The Digital Radon Transform

The Radon transform for discretely given points of a g function at points
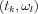$$ \left (t_{k},\omega _{l} \right )$ in sinogram space:
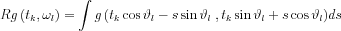
$$ Rg \left (t_{k},\omega _{l} \right )=\int g \left ( t_{k}\cos \vartheta _{l} -s\sin \vartheta _{l}\right, t_{k}\sin \vartheta _{l} +s\cos \vartheta _{l} \right ))ds$
Approxiomately:
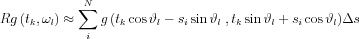
$$ Rg \left (t_{k},\omega _{l} \right )\approx \sum_{i}^{N} g \left ( t_{k}\cos \vartheta _{l} -s_{i}\sin \vartheta _{l}\right, t_{k}\sin \vartheta _{l} +s_{i}\cos \vartheta _{l} \right ))\Delta s$
where
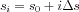
$$s_{i}=s_{0}+i\Delta s$
With this notation for each i we need to interpolate the function g in 2D. If we choose the step size such that in dimension x we match grid points we can spare the interpolation step. Let us do the integration according to x:
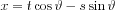
$$ x=t\cos \vartheta -s\sin \vartheta$
thus:
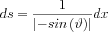
$$ ds=\frac{1}{\left | -sin\left ( \vartheta \right ) \right |}dx$
With that:
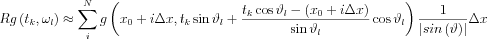
$$ Rg \left (t_{k},\omega _{l} \right )\approx \sum_{i}^{N} g \left ( x_{0}+i\Delta x, t_{k}\sin \vartheta _{l} +\frac{t_{k}\cos \vartheta _{l}-\left ( x_{0}+i\Delta x \right )}{\sin \vartheta _{l}}\cos \vartheta _{l} \right )\frac{1}{\left | sin\left ( \vartheta \right ) \right |}\Delta x$

From this from we see that if the angle falls around 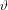$$ \vartheta$ 0 or 180⁰,the expression renders unstable, and we should rather swith to mathcing grid lines in the y dimension.

Export

Medical Imaging

Site Language: English

The Digital Radon Transform

Sidebar

Medical Imaging

Site Language: English