Multidimensional Central Slice Theorem and the Fourier Inverson Formula

The Central Slice Theorem in multiple dimensions is in full analogy with the 2D version with the notations introduced earlier. Let 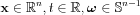$$\mathbf{x}\in \mathbb{R}^{n}, t\in \mathbb{R} , \boldsymbol{\omega}\in \mathbb{S}^{n-1}$ . The n-dimensional function Radon transformed and Fourier transformed according to the t variable reads:
$$ \mathfrak{F}_{t}\left [\mathfrak{R}f\left ( t,\boldsymbol{\omega} \right ) \right ]\left ( r,\boldsymbol{\omega} \right )=\int_{-\infty }^{\infty }\mathfrak{R}f\left ( t,\vartheta \right )e^{-itr}dt=\int_{-\infty }^{\infty }\int_{-\infty }^{\infty }f\left ( t\boldsymbol{\omega} +\mathbf{y} \right )e^{-itr}dtd\mathbf{y}$

Let us change variables 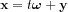$$\mathbf{x}=t\boldsymbol{\omega}+ \mathbf{y}$ for the integration, that means the rotation of the vector (t,y₁,y₂...,y_n-1) , therefore its Jacobian equals to 1.
Then:
$$\mathfrak{F}_{t}\left [\mathfrak{R}f\left ( t,\boldsymbol{\omega} \right ) \right ]\left ( r,\boldsymbol{\omega} \right )=\int_{-\infty }^{\infty }f\left ( \mathbf{x} \right )e^{-i\boldsymbol{\omega}\mathbf{x}r}d\mathbf{x}= \mathfrak{F}_{\mathbf{x}}\left [\mathfrak{R}f\left ( t,\boldsymbol{\omega} \right ) \right ]\left ( r\boldsymbol{\omega} \right )$
thus in the multidimensional case Fourier transform in the affine parameter gives a full Fourier transform in an n-dimensional polar coordinate system. .

The Fourier inversion Formula in an n-dimensional form

Let us carry out the inverse Fourier transform and insert the result of the Central Slice Theorem:
$$ f(\mathbf{x})=\left (\frac{1}{2\pi} \right )^{n-1}\int_{-\infty}^{\infty} \mathfrak{F}\left [ f \right ]\left ( \boldsymbol{\xi }\right )e^{i\mathbf{x} \boldsymbol{\xi }} d\boldsymbol{\xi } = \frac{1}{2}\left (\frac{1}{2\pi} \right )^{n-1}\int_{\mathbb{S}^{n-1}}\int_{-\infty}^{\infty} \mathfrak{F}_{t}\mathfrak{R}f\left \left ( r\boldsymbol{\omega} )\left | r \right |^{n-1} e^{ir\mathbf{x} \boldsymbol{\omega }}dr d\boldsymbol{\omega }$
where we have changed the coordinate system to polar. To match the two sides of the equation we have also changed the domain of integration from the domain $$\left [ 0,\infty \right ]$ to $$\left [ -\infty,\infty \right ]$ , and made up for it with a factor of two. This is more a didactic than a mathematical necessity, in order to show the singularity in the origin of the frequency domain.
The manipulations done locally in the frequency domain show global effect in the spatial domain (think about adding a single frequency component), so a singularity null-sized frequency domain is not negligible at all.

In the next section we will try to interpret the expressions above.

Export

Medical Imaging

Site Language: English

Multidimensional Central Slice Theorem and the Fourier Inverson Formula

The Fourier inversion Formula in an n-dimensional form

Sidebar

Medical Imaging

Site Language: English