Example: 1D imaging of two spots

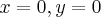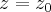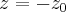Here we present an example of the concept detailed in the previous section. Assume we have two spot-like samples in the $x=0, y=0$ plane in the positions $z=z_0$ and $z=-z_0$ . Let's use a simple FID sequence with constant $z$ gradient right after the pulse, during the acquisition. The sequence diagram is shown in Figure 1.

Figure 1. Left: two spot samples to be imaged. Right: Sequence diagram of a simple 1D imaging FID with constant readout gradient.

The phase evolution of the spins in the two samples with a gradient strength 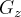$G_z$ :

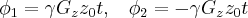$\label{1D_imaging1} \phi_1 = \gamma G_z z_0 t, \hspace{10pt} \phi_2 = -\gamma G_z z_0 t$ (1)

Their complex demodulated signal:

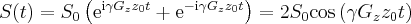$\label{1D_imaging2} S(t) = S_0 \left(\mathrm{e}^{\mathrm{i} \gamma G_z z_0 t} + \mathrm{e}^{- \mathrm{i} \gamma G_z z_0 t} \right) = 2 S_0 \mathrm{cos} \left( \gamma G_z z_0 t \right)$ (2)

The spatial frequency vector 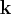$\mathbf k$ now only has $z$ component:

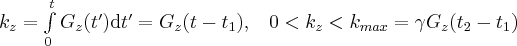$\label{1D_imaging3} k_z = \gammabar \int \limits_0^t G_z(t') \mathrm d t' = \gammabar G_z (t-t_1), \hspace{10pt} 0 < k_z < k_{max}= \gamma G_z (t_2-t_1)$ (3)

Hence the signal as a function of spatial frequency:

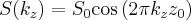$\label{1D_imaging4} S(k_z) = S_0 \mathrm{cos} \left(2 \pi k_z z_0 \right)$ (4)

The spatial spin density is obtained by the inverse Fourier transform of the signal, now only in one dimension.

$\label{1D_imaging5} \rho(z) = \int \mathrm d k_z 2 S_0 \mathrm{cos} \left( 2 \pi k_z z_0 \right ) \mathrm{e}^{-\mathrm i 2 \pi k_z z} = S_0 \int \limits_{- \infty}^{\infty} \mathrm d k_z \left(\mathrm{e}^{\mathrm i 2 \pi k_z (z+z_0)} + \mathrm{e}^{\mathrm i 2 \pi k_z (z-z_0)} \right)= \\ = S_0 \left [ \delta (z+z0) + \delta (z-z_0) \right]$ (5)

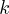As can be seen, the inverse Fourier transformed signal gives back the original spot-like spin density along the $z$ direction.The illustration of the signal and the trajectory in $k$ -space are shown in Figure 2.

Figure 2. Upper left: Laboratory signal of the two spot-like samples with its envelope. Lower left: Real part of the demodulated signal forming a cosine. Right: trajectory in k-space. Note that the maximal reached k value is proportional to the acquisition (or sampling) time Ts.

Export

Medical Imaging

Site Language: English

Example: 1D imaging of two spots

Sidebar

Medical Imaging

Site Language: English