Inverse transformation method for linear invariant systems

Book for Physicists » Introduction to the mathematics of medical imaging » Mathematical Methods of Linear Model Based Image Processing Procedures » Laplace-Transformation » Inverse transformation method for linear invariant systems

If the Laplace transformation of the input function can be written in rational function (it is a valid condition in many cases, such as Dirac-delta, Heavyside unit step function, harmonic step functions /like sin, cos/,….etc.), then the output response function in the extended complex frequency domain can be expressed as follow:

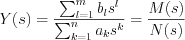$$Y(s) = \frac{\sum_{l=1}^{m}b_{l}s^{l}}{\sum_{k=1}^{n}a_{k}s^{k}} = \frac{M(s)}{N(s)}$ which is rational function.

If 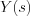$Y(s) is proper rational function, then 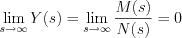$$\lim_{s \rightarrow \infty} Y(s) = \lim_{s\rightarrow \infty} \frac{M(s)}{N(s)} = 0$ . . If 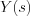$Y(s) is improper rational function, then by means of polynomial divides is possible to obtain

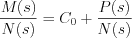$$\frac{M(s)}{N(s)} = C_{0} + \frac{P(s)}{N(s)}$ ,where 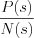$$\frac{P(s)}{N(s)}$ already is a proper rational function.

Consequently 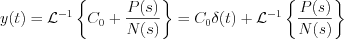$$y(t) = \mathcal{L}^{-1}\left\{ C_{0} + \frac{P(s)}{N(s)}\right\} = C_{0}\delta (t) + \mathcal{L}^{-1}\left\{\frac{P(s)}{N(s)}\right\}$

Only those cases will be considered in the following chapter, where the inverse transformation may be executed by proper rational functions.

Export

Medical Imaging

Site Language: English

Inverse transformation method for linear invariant systems

Sidebar

Medical Imaging

Site Language: English