Inverse Radon transfrom with Riesz potentials

The Fourier inversion formula simply lead us the filtering with |r| in the frequency domain and its alternative formulation with the differential and Hilbert transform operators. Using the Riesz potentials we can give a family of solutions where the Fourier inversion formula is just one of the members.

The 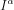$$ I^{\alpha }$ Riesz-potential can be defined of a function of n-dimensions as follows:
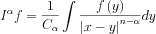
$$ I^{\alpha }f=\frac{1}{C_{\alpha }}\int \frac{f\left ( y \right )}{\left | x-y \right |^{n-\alpha }}dy$
Here 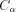$$ C_{\alpha }$ is a constant. Similarly to the Hilbert transform we can give a definition using the Fourier transform:
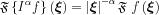
$$ \mathfrak{F}\left \{ I^{\alpha } f \right \} \left ( \boldsymbol{\xi } \right )= \left | \boldsymbol{\xi } \right |^{-\alpha }\mathfrak{F}\ f \left ( \boldsymbol{\xi } \right )$

Here 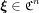$$ \boldsymbol{\xi } \in \mathfrak{C}^{n}$ .
From this definition we can see
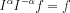
$$ I^{\alpha }I^{-\alpha }f=f$
Let us write the Riesz-potential of f with the Fourier definition:
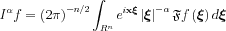
$$ I^{\alpha }f=\left ( 2\pi \right )^{-n/2}\int_{R^{n}} e^{i\mathbf{x}\boldsymbol{\xi }}\left | \boldsymbol{\xi } \right |^{-\alpha }\mathfrak{F}f\left ( \boldsymbol{\xi } \right )d \boldsymbol{\xi }$

Let us change variables to an n-dimensional polar coordinate system with notations:
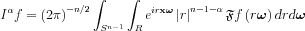
$$ I^{\alpha }f=\left ( 2\pi \right )^{-n/2}\int_{S^{n-1}}\int_{R} e^{ir\mathbf{x}\boldsymbol{\omega }}\left | r \right |^{n-1-\alpha }\mathfrak{F}f\left ( r\boldsymbol{\omega } \right )drd\boldsymbol{\omega }$
Let us fill in the result of the multidimensional Central Slice Theorem:
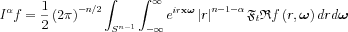
$$ I^{\alpha }f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}\int_{S^{n-1}}\int_{-\infty }^{\infty} e^{ir\mathbf{x}\boldsymbol{\omega }}\left | r \right |^{n-1-\alpha }\mathfrak{F}_{t}\mathfrak{R}f\left ( r,\boldsymbol{\omega } \right )drd\boldsymbol{\omega }$
With operator notations we can write:
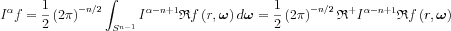
$$ I^{\alpha }f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}\int_{S^{n-1}} I^{\alpha-n+1 }\mathfrak{R}f\left ( r,\boldsymbol{\omega } \right )d\boldsymbol{\omega }=\frac{1}{2}\left ( 2\pi \right )^{-n/2}\mathfrak{R}^{+} I^{\alpha-n+1 }\mathfrak{R}f\left ( r,\boldsymbol{\omega } \right )$

On both sides calculating the $$ I^{-\alpha }$ potentials:
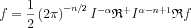
$$ f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}I^{-\alpha }\mathfrak{R}^{+} I^{\alpha-n+1 }\mathfrak{R}f\left$
and from that several inversion formulae can be obtained.

In the case of 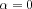$$ \alpha=0$ we get back the earlier shown inversion formula. It is worthwhile to highlight the case of 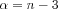$$ \alpha=n-3$ now
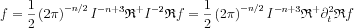
$$ f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}I^{-n+3 }\mathfrak{R}^{+} I^{-2}\mathfrak{R}f\left=\frac{1}{2}\left ( 2\pi \right )^{-n/2}I^{-n+3 }\mathfrak{R}^{+} \partial _{t}^{2}\mathfrak{R}f\left$

which at least partially reinstates locality of the inversion formula.

Export

Medical Imaging

Site Language: English

Inverse Radon transfrom with Riesz potentials

Sidebar

Medical Imaging

Site Language: English