Linear shift invariant system description by the step response function
Applying of the step response function in order to characterize the property of the linear shift invariant system is a very often used method.
Definition: Output response of a linear shift invariant system by the Heavyside unit step function is called step response function:
Heavyside unit step function 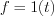
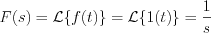
Consequently the output response function:
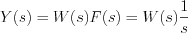
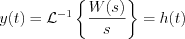 is called step response function.
is called step response function.
It is possible to see, the relation between the step response function and the transfer function in the extended complex frequency domain is as follow:
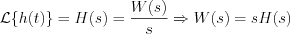 , where the transfer function was derived by the step response function.
, where the transfer function was derived by the step response function.
Furthermore, next question is arisen: step response function of a linear shift invariant system is known in the real parameter space. How is it possible to get the output response for  general step function.
general step function.
As it is known from previously:
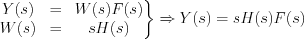
Let’s execute Laplace transformation of both sides:
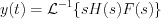
Apply the operation rules of Laplace transformation
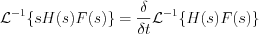
,where 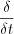 is the weak derivative.
is the weak derivative.
The output response function can be determined by the step response function as follow:
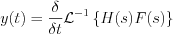
Apply the convolution rule for the product functions:
![$ y(t)= \frac{\delta }{\delta t} \int_0f(\tau)h(t-\tau)d\tau= \frac{\delta }{\delta t} \left \[f(t)\ast h(t) \right \]](lib/equation/pictures/8e5ef96ec2feaa6e07d5d73645dd9d2f.png)
( by click here see the detailed driving)
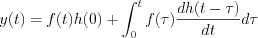 , where
, where 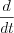 means the regular derivative.
means the regular derivative.
The output response determined by step response function is called Duhamel-theorem.