Példa a kvázisztatikus elasztográfia egyenletrendszerének numerikus megoldására

Book for Physicists » Ultrasound » Új irányok az ultrahang diagnosztikában » Szonoelasztográfia » Deformációs elasztográfia » Példa a kvázisztatikus elasztográfia egyenletrendszerének numerikus megoldására

Bizonyos határfeltételek mellett milyen, a következő, viszonylag jól programozható eljárással ismerhetjük meg az elasztikus modulus értékét a szövetekben.
Tételezzük fel, hogy a vizsgált szövet belsejében valamilyen jól körülhatárolt inhomogenitás található. Ebben az esetben a Young-modulus, és így $\mu$ értéke nem folytonos függvénye a helynek, hanem az adott inhomogenitás határán véges szakadással rendelkezik. Egy valódi vizsgálat, például rákos daganat keresése esetén jó közelítéssel teljesül ez a feltétel, és egy ilyen mérés során a feladat nem csupán a tumor Young-modulusának meghatározása, hanem pontos helyének és alakjának feltérképezése is.
Tehát a legtöbb valódi esetben a fenti négy egyenlet mellett adott határfeltételünk a következő: egyensúlyban az inhomogenitás határán a mechanikai feszültség felületre normális része azonos kell legyen a határon belül és kívül. Azaz: 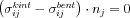$\left ( \sigma_{ij}^{kint}-\sigma_{ij}^{bent} \right )\cdot n_{j}=0$ , ahol 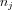$n_{j}$ a határfelület egységnyi hosszúságú normálvektora a határ valamely pontjában. Behelyettesítve a feszültségtenzor már megismert egyszerűsített alakját: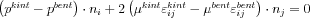 $\left ( p^{kint}-p^{bent} \right )\cdot n_{i}+2\left ( \mu^{kint}\varepsilon_{ij}^{kint}-\mu^{bent}\varepsilon_{ij}^{bent}\right )\cdot n_{j}=0$
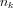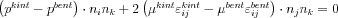Mivel ebben a levezetésben a nyomás értékéről semmilyen feltételezéssel nem élünk, ezért az imént összevont alakban felírt (i=1,2,3 esetén) három egyenletből álló egyenletrendszerből azt ki kell ejtenünk. Ha a fenti alakot beszorozzuk $n_{k}$ -val: $\left ( p^{kint}-p^{bent} \right )\cdot n_{i} n_{k}+2\left ( \mu^{kint}\varepsilon_{ij}^{kint}-\mu^{bent}\varepsilon_{ij}^{bent}\right )\cdot n_{j} n_{k}=0$ . Könnyen belátható, hogy a j-re való összegzést elvégezve, például i=1 és k=2 esetén a nyomást tartalmazó tagok azonosak lesznek az i=2 k=1 indexekkel felírt egyenletbeli tagokkal, így a két egyenletből már kiejthetők: 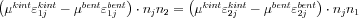$\left ( \mu^{kint}\varepsilon_{1j}^{kint}-\mu^{bent}\varepsilon_{1j}^{bent}\right )\cdot n_{j} n_{2}=\left ( \mu^{kint}\varepsilon_{2j}^{kint}-\mu^{bent}\varepsilon_{2j}^{bent}\right )\cdot n_{j} n_{1}$ , hasonlóan nyerhető egy független egyenlet az 1-3 indexpár felhasználásával. Az egyenletrendszer tehát:
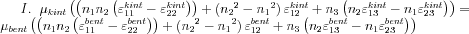
$I.\;\; \mu_{kint}\left( \left ( n_{1}n_{2}\left ( \varepsilon_{11}^{kint}-\varepsilon_{22}^{kint} \right ) \right )+\left ( {n_{2}}^{2}-{n_{1}}^{2} \right )\varepsilon_{12}^{kint}+n_{3}\left(n_{2}\varepsilon_{13}^{kint}-n_{1}\varepsilon_{23}^{kint}\right)\right )=\mu_{bent}\left( \left ( n_{1}n_{2}\left ( \varepsilon_{11}^{bent}-\varepsilon_{22}^{bent} \right ) \right )+\left ( {n_{2}}^{2}-{n_{1}}^{2} \right )\varepsilon_{12}^{bent}+n_{3}\left(n_{2}\varepsilon_{13}^{bent}-n_{1}\varepsilon_{23}^{bent}\right)\right )$
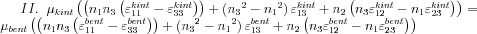
$II.\;\; \mu_{kint}\left( \left ( n_{1}n_{3}\left ( \varepsilon_{11}^{kint}-\varepsilon_{33}^{kint} \right ) \right )+\left ( {n_{3}}^{2}-{n_{1}}^{2} \right )\varepsilon_{13}^{kint}+n_{2}\left(n_{3}\varepsilon_{12}^{kint}-n_{1}\varepsilon_{23}^{kint}\right)\right )=\mu_{bent}\left( \left ( n_{1}n_{3}\left ( \varepsilon_{11}^{bent}-\varepsilon_{33}^{bent} \right ) \right )+\left ( {n_{3}}^{2}-{n_{1}}^{2} \right )\varepsilon_{13}^{bent}+n_{2}\left(n_{3}\varepsilon_{12}^{bent}-n_{1}\varepsilon_{23}^{bent}\right)\right )$
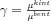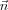Látható, hogy ha ismertnek feltételezzük a deformációtenzor elemeinek értékét, akkor a fenti egyenletekben csupán a felületre merőleges egységvektor komponensei, illetve a $\gamma=\frac{\mu^{kint}}{\mu^{bent}}$ arány ismeretlen. Nyilvánvaló, hogy homogén anyagot vizsgálva a $\gamma$ hányados értéke tetszőleges $\vec{n}$ irány esetén egy, mivel $\mu$ homogén esetben konstans. Ugyanúgy, ha $\mu$ folytonosan, és a mérésünk felbontásához képest kellően lassan változik, a hányados értéke továbbra is egy marad. 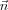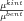Azonban egy határbeli pontban nézve tetszőleges irányítású $\vec{n}$ esetén a $\gamma$ -ra kapott érték jelentősen eltér egytől, bár csak a valódi normálvektor komponensekkel számítva egyezik meg $\frac{\mu^{kint}}{\mu^{bent}}$ pontos értékével.
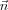Ezt a tulajdonságot felhasználva a fenti egyenletrendszer $\gamma$ -ra numerikusan megoldható két lépésben: először tetszőleges $\vec{n}$ irányokkal végigpásztázzuk a mintát, így a 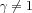$\gamma\neq 1$ feltételből megkapjuk a határ pontjainak koordinátáit, majd második lépésben a határ alakjának és helyének ismeretében már valóban a vizsgált felületre merőleges egységvektorok koordinátáival kiszámíthatjuk az egyes pontokban $\gamma$ értékét.
Természetesen az itt ismertetett eljáráson kívül számos más módszert is leírtak már a négy egyenletes differenciálegyenlet-rendszer és határfeltételeinek kielégítésére, azonban mivel az egyenletek egzakt megoldása nem lehetséges, minden ismert eljárás óriási számítástechnikai kapacitást igényel, mégis meglehetősen nagy hibával terhelt.

Export

Medical Imaging

Site Language: English

Példa a kvázisztatikus elasztográfia egyenletrendszerének numerikus megoldására

Sidebar

Medical Imaging

Site Language: English