Properties of the Fourier Transform
One-dimensional Fourier Transformation is defined as follows:
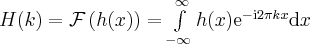 (1)
(1)
We mention here that the domain of this transformation is the set of functions whose absolute value has a finite integral over 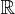 but hereinafter we will always suppose that the picked function is element of this set as in practice we will deal with finite functions limited in a finite time interval, and therefore their absolute value can always be integrated.
but hereinafter we will always suppose that the picked function is element of this set as in practice we will deal with finite functions limited in a finite time interval, and therefore their absolute value can always be integrated.
The inverse Fourier transformation is very similar to the transformation itself, they only differ in a complex conjugate:
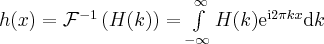 (2)
(2)
The frequently used properties of the Fourier Transform are the followings:
1) Linearity:
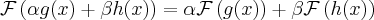 (3)
(3)
for every complex numbers 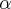 and
and 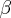 . Specifically, a constant phase multiplication is preserved during the Fourier transform.
. Specifically, a constant phase multiplication is preserved during the Fourier transform.
2) Shifting:
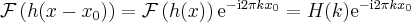 (4)
(4)
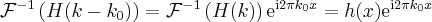 (5)
(5)
For every real 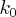 and
and 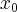 . This means that a linear phase ramp in the Fourier space (
. This means that a linear phase ramp in the Fourier space (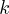 -space) results a spatial shift in the image space and vice versa. The shift is proportional to the steepness of the phase ramp.
-space) results a spatial shift in the image space and vice versa. The shift is proportional to the steepness of the phase ramp.
3) Convolution:
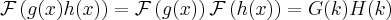 (6)
(6)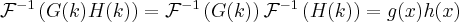 (7)
(7)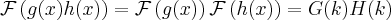 (8)
(8)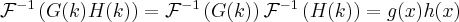 (9)
(9)
In other words, a multiplication in the 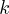 -space results as a convolution in the image space with the inverse Fourier transformed version of the multiplying function. In the other direction, a convolution in the
-space results as a convolution in the image space with the inverse Fourier transformed version of the multiplying function. In the other direction, a convolution in the 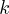 -space means a multiplication in the image space.
-space means a multiplication in the image space.
4) Symmetry. If 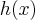 is a real function then:
is a real function then:
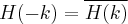 (10)
(10)
This symmetry is of utmost importance in the so-called partial Fourier imaging where the effective spin density is assumed to be real, and therefore the 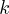 -space data is redundant as negative
-space data is redundant as negative 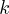 -vector values can be replaced by the complex conjugate of the positive
-vector values can be replaced by the complex conjugate of the positive 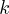 -vector values.
-vector values.
The extension of the upper properties to higher dimensions can be done quite intuitively. The variables are then vectorial denoted by  and
and 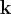 , and the Fourier Transform (for example in 3D) is defined by the following with
, and the Fourier Transform (for example in 3D) is defined by the following with 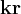 equals to their dot product:
equals to their dot product:
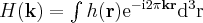 (11)
(11)