Characteristic Input Functions
„Heavyside” unit step function is one of the most important and most frequently used input function at the system analysis. Figure 8. presents both the curve and mathematical description of the function.
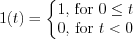
Figure 9. shows the curve and the mathematical description of the shifted unit step function:
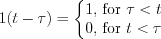
Impulse function (Dirac-delta)
Let’s consider Figure 10. for the introduction of ideal impulse function.
Basic property of the 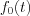 function:
function:
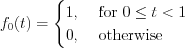
As well as 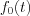 should satisfy the following condition:
should satisfy the following condition: 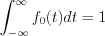 too.
too.
Define 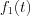 function in the following way (see Figure 10.)
function in the following way (see Figure 10.)
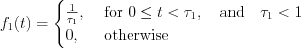
Consequently is possible to see 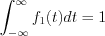 .
.
Define similar way 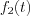 and then
and then 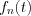 .
.
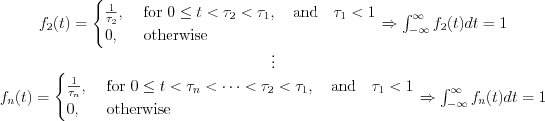
Determine the limit as follow:
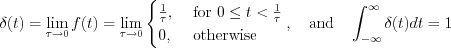
The obtained  function is called Dirac-delta, Dirac impulse, unit impulse function. Main feature of Dirac-delta is, everywhere in the
function is called Dirac-delta, Dirac impulse, unit impulse function. Main feature of Dirac-delta is, everywhere in the  interval is zero except in
interval is zero except in  point, where value of the function i.e. the “amplitude” is infinite, while the improper integral value i.e. “the intensity” is 1.
point, where value of the function i.e. the “amplitude” is infinite, while the improper integral value i.e. “the intensity” is 1.
Let’s define the shifted Dirac-delta function as follow (see Figure 11.).
The shifted Dirac-delta can be expressed by using the above mentioned definitions and interpretations as follow:
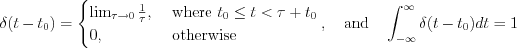
The shifted  function is presented on the Figure 12. :
function is presented on the Figure 12. :
Let’s attempt to find relation between the “Heaviside” unit step function and Dirac-delta unit impulse function. Let’s consider the set of continuously differentiable functions in the 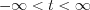 interval at first:
interval at first:
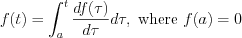
According to the classical mathematical analysis Heavyside unit step function cannot be continuously
differentiable in the 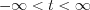 interval, i.e.
interval, i.e.

Let’s consider the Figure 13. in order to make relation between the Dirac delta unit impulse function and Heavyside unit step function.
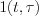 function can be described in the following way:
function can be described in the following way:
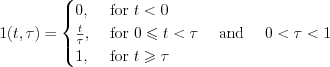
The relation between the Heavyside function and the 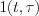 is as follow:
is as follow:
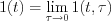
Consequently the derivative of 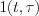 function by
function by 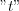 variable is.
variable is.
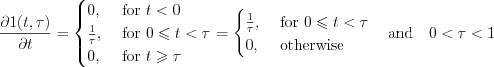
Since variable  has changed in the (0,1) interval, consequently
has changed in the (0,1) interval, consequently 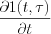 derived function resulted same
derived function resulted same
impulse function with unit area (i.e. intensity) as was discussed above at the explanation of Dirac-delta.
Apply the following denoting:
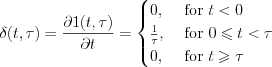
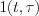 and
and 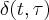 have the following relation too.
have the following relation too.
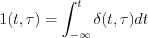
Consequently, determine the following limit:
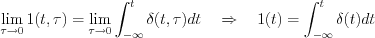
It is possible to say, the derivative of Heavyside unit step function is defined at 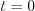 point, as follows:
point, as follows:
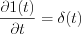
The operation is called weak derivative and it is denoted by 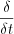 .
.
Next will be discussed several consequences of Dirac-delta and the weak derivative.
Let 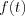 continuously differentiable function in the
continuously differentiable function in the 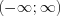 interval. The value of
interval. The value of 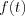 at
at 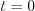 point can be determined by Dirac-delta as follow
point can be determined by Dirac-delta as follow
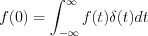
Value of the same 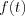 function at any
function at any 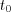 point within the
point within the 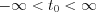 interval can be determined by the shifted Dirac delta:
interval can be determined by the shifted Dirac delta:
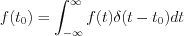
Let’s define the analysis of that function set having finite “jump” discontinuities within the domain. (see Figure 14.)
![$
f(t)=\begin{cases}
f_1(t),\quad \text{for}\quad t>t_0 \quad \text{and}\quad f_1(t)\quad \text{ is continuously differentiable in the } (t_0;\infty) \text{ interval}\\
f_2(t) ,\quad \text{for}\quad t \leq t_0 \quad \text{and}\quad f_2(t)\quad \text{ is continuously differentiable in the } (-\infty;t_0] \text{ interval}
\end{cases}](lib/equation/pictures/6121a96fbe64bcbd9b5100fe78537abd.png)
The finite discontinuity of 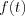 function at
function at  point should be satisfied the following condition
point should be satisfied the following condition
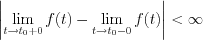 Consequently, the derivative of
Consequently, the derivative of 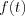 function can be described by the weak derivative in the
function can be described by the weak derivative in the 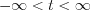 interval as follow:
interval as follow:
![$
\frac{\delta f(t)}{\delta t}=\begin{cases}
\frac{df_1(t)}{dt}, \quad \text{ for } \quad t_0<t \\
\\
\left [\lim_{t \to +t_0} f(t)- \lim_{t \to -t_0} f(t) \right ]\delta(t-t_0), \quad \text{ for } \quad t_0=t \\
\\ \frac{df_2(t)}{dt}, \quad \text{ for } \quad t<t_0
\end{cases}](lib/equation/pictures/095e8722bbba55108a6d2fe82b679e20.png)
The weak derivative function can be presented as follow (Figure 15.).
![$
\frac{\delta f(t)}{\delta t}=\begin{cases}
\frac{df_1(t)}{dt},\quad \text{for} \quad t_0<t \\
\\
I\delta(t-t_0),\quad \text{for} \quad t_0=t, \\
\\
\frac{df_2(t)}{dt},\quad \text{for} \quad t<t_0
\end{cases}\quad \text{where}\quad I=\left [\lim_{t \to +t_0} f(t)- \lim_{t \to -t_0} f(t) \right ]](lib/equation/pictures/fef752a9200d35e9467f21b9537847dd.png)
Periodic Function
Stationary state of any linear systems is investigated very often by periodic input signal. 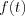 function is periodic by
function is periodic by 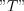 , if
, if 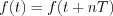 , where
, where 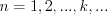 Natural numbers (see Figure 16.)
Natural numbers (see Figure 16.)
Periodicity of the function is 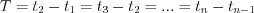
According to the Fourier theory any 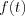 periodic function can be approximated by the following series:
periodic function can be approximated by the following series:
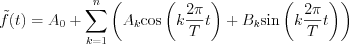
Maximal error of the approximation is: 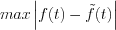 . Let’s introduce
. Let’s introduce 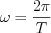 generalized cycle frequency
generalized cycle frequency
(See the detailed at Appendix: Deriving of Fourier Theory, Fourier Series):
Consequently, 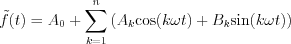
Next problem is arisen: is it possible to expand 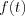 by infinite trigonometric series
by infinite trigonometric series
If 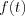 consistently convergent in the
consistently convergent in the 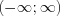 interval, then
interval, then 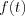 function can be expanded by Fourier series as follow
function can be expanded by Fourier series as follow
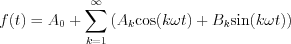 , where
, where 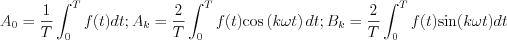 .
.
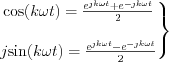 by means of these Euler formulas
by means of these Euler formulas 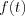 can be written as follow
can be written as follow
(See the detailed at Appendix: Description of Fourier Series by complex expression) :
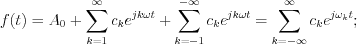 ahol
ahol 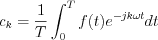
The next examples illustrate, how are presented the above described characteristic and periodic input functions in the imaging. The illustration are the response functions of 2D emission imaging systems (they are created by round shape detector gamma cameras)
The original document is available at http://549552.cz968.group/tiki-index.php?page=Characteristic+Input+Functions