Deriving of Duhamel Theorem
Deriving of Duhamel-theorem will be executed in the followings.
Let’s start from the weak derivative of convolution
![$ y(t) = \frac{\delta }{\delta t} \left \[ f(t)\ast h(t) \right \]](lib/equation/pictures/0151c9d489516f837f9cf5e9b0972881.png)
Apply the following denoting:
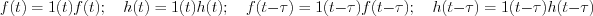
Let’s describe the convolution formula in the argument of weak derivative:
![$ y(t) = \frac{\delta }{\delta t}\int_0^tf(\tau)h(t-\tau)1(t-\tau)d\tau=\int_0^tf(\tau) \frac{\delta }{\delta t}\left [ h(t-\tau)1(t-\tau) \right ] d\tau](lib/equation/pictures/a67e8550c0784986064f8faae7de9a8e.png)
![$ y(t)= \int_0^tf(\tau) \left [ h(t-\tau) \frac{\delta 1(t-\tau)}{\delta t}+ 1(t-\tau) \frac{dh(t-\tau)}{dt} \right ] d\tau](lib/equation/pictures/4aa1db259dd32f9abf184d93f972ceb2.png)
![$ y(t)= \int_0^tf(\tau) \left [ \delta(t-\tau)h(t-\tau) +1(t-\tau) \frac{dh(t-\tau)}{dt} \right ] d\tau](lib/equation/pictures/1d653d249b6f2deaa2bdf10097c29cac.png)
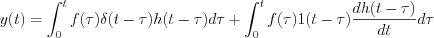
If 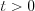
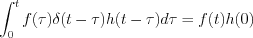 , and
, and
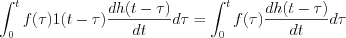 , where
, where 
Now, it is possible to get the final expression of Duhamel-theorem
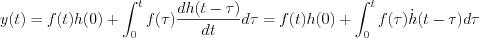 , where
, where  means the conventional derivative, which is denoted by “
means the conventional derivative, which is denoted by “ ” as usual.
” as usual.
Return to the ’Linear shift invariant system description by step response function’ chapter
The original document is available at http://549552.cz968.group/tiki-index.php?page=Deriving+of+Duhamel+Theorem