Elements of radiology imaging
According to the 1. Chapter, while X-ray is propagating through a matter it is absorbed corresponding to the known Beer-Lambert law (Equation 10). Different parts of the beam travelling through different absorber layers are attenuated with different degree depending on the absorption coefficient of the irradiated sample volume. The X-ray beam after it propagates through the object is detected on a plane which is approximately perpendicular to the direction of the propagation. This two-dimensional plane section carries information about the absorption parameters of the irradiated layer. The theory of radiology imaging based on absorption is demonstrated on Figure 17.
The projected image contains different shades of gray matching with a scale corresponding also to universal principles and the human sensation. This scale was named after the inventor of CT, G. N. Hounsfield:
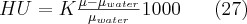
where the whole scale is represented by the interval (-1000, 3000). This wide gray scale of course cannot be resolved by human eye, since it can make difference only between 30-40 shades. Table 3 contains the HU values of tissues. So-called windowing technique could be used in order to differentiate certain parts of the gray pattern projected on Hounsfield scale by human eyes. Displaying only that part of the whole scale which is necessary to the examination the disturbing parts can be excluded. In this case, the shades of gray can be differentiated in the windowed section, i.e. if inside the window a smaller interval is chosen as the gray scale than the interval of the whole HU scale, then the shades in this more narrow HU scale can be distinguished by eyes.
Table 2. Hounsfield values of different matters and tissues. Különböző anyagok és szövetek Hounsfield-értékei
| Air | Lung | Soft tissues | Adipose tissue | Water | Blood | Muscle | Contrast materials | Bone |
| -1000 | -700 | -100 | -84 | 0 | +30 | +40 | +100 | +700 |
| +300 | +45 | +1000 | +3000 |
The middle of the window should be adjusted to the corresponding part of the scale depending on which interval from Table 2 is chosen by the Hounsfield unit of the examined object.
Figure 18 demonstrates the application of the window, where (a) picture is made by a window optimized for brain tissue and (b) picture shows the window used for skull examination.
The image gained from a radiology imaging, contains the integral of the absorption properties of the media irradiated by x-rays.
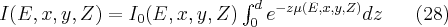
Equation 28 gives the attenuation effect of a layer with a d width and µ absorption coefficient at a given geometrical point and at E energy. According to this, the result of the x-ray projection depends on the position of the examined point (in the plane perpendicular to the projection) and the x-ray’s energy distribution through the energy dependence of the absorption coefficient. The absorption coefficient is generally decreases with the increase of the x-ray’s energy and increases with the atomic number of the absorber. Therefore, the absorption media attenuates selectively the irradiation beam depending on the constitution. During the propagation through the same matter, larger portion of the low-energy spectral range’s intensity is absorbed than the one of the high-energy range. This means that the spectral distribution of the projecting beam should be adjusted to the examined tissue type. In the case of a strong absorber the low-energy components do not contribute to the projection, since their larger portion is absorbed partially or entirely. Moreover, this procedure increases only the absorbed dose without contributing to the birth of the image. On the contrary, in the case of tissues with lower attenuation features (e.g. soft tissue), during a projection the high-energy components are hardly attenuated, i.e. the result contains little information about the sample’s interior. Thus components with lower energy should be used for the irradiation.
One possibility to affect the components of x-ray’s spectrum is the change of the x-ray tube’s voltage which influences the shape of the x-ray spectrum. The other opportunity is to place a filter with a certain width and matter in the way of the irradiating beam between the x-ray tube and the object.
The filter attenuates selectively the parts of the spectrum corresponding to their energy due to their energy depending absorption. Since the elements’ absorption function is described with a quite complicated mathematic formula, its effect on the shape of the x-ray spectrum is really variable depending on the components of the filter. So it can result actually in any arbitrary shape of the spectrum. Figure 20 demonstrates a few of these cases, where spectra of a low-powered (4W) transmission x-ray tube used for analytic purposes can be seen with 40 kV anode voltage and with filters having different widths and matters.
The characteristic lines of the anode’s matter can be recognized in the spectrum as well (Ag-Kα, Ag-Kβ). In the case of Cu and Mo, the effect of absorption edges can be observed as the fast changes of the spectrum, even with orders. The following pages help in the calculation of the transmission and absorption coefficients: http://physics.nist.gov/cgi-bin/Xcom/xcom2![]() and http://henke.lbl.gov/optical_constants/
and http://henke.lbl.gov/optical_constants/![]()
Inside the matter irradiated by x-ray beam different interactions can occur between the x-ray photons and the atomic electrons. One type of them is the scattering phenomena where the direction of the emitted photon does not parallel with the direction of the incident photon (see Equation 5 and Figure 2). So, the larger the Compton scattering’s probability is inside the examined object, the more photon propagates in a direction which differs from the original one, i.e. worsens the quality. Thus, to the image points lots of photons arrive travelling on a non-straight path and the information carried by them does not originate from the atoms in the direction of the propagation. The result of such a projection contains many blurry area, and regions with decreased contrast. The image quality worsening effect can be decreased by specially constructed collimators.
The simplest collimator is a simple tube whose axis is parallel with the projection’s axis. So the arriving photons deviating with a large angle from this axis (e.g. because of Compton scattering) collide with the tube’s wall and are absorbed.
Collimators with adjustable size are commonly used in order to optimize them to the size and absorption properties of the examined object. It is composed by four absorber layers with high atomic number whose positions can be set by motors. With this technique, the irradiated area can be chosen and the others can be kept in shadow. The other frequently used tool is the grid whose effect on the projecting x-ray beam is similar to the one of the tube thanks to its structure. Since the grid is equal with many tubes placed next to each other, the image quality increasing effect described above appears at the entire cross section. The grids can be classified into two main groups: (a) Grids with classical structure. In this case, layers with low and high absorption are placed alternatively next to each other.
(b) Square grid containing empty cells. It has significantly larger transmission meaning a lot lower absorption of the projecting x-rays, but the collimator effect still appears thanks to the matter of the grid with high absorption (Pb, W). Typical grid sizes: 4-5 mm width, 8-10mm height, 1mm distance between grid elements. The collimator effect can be optimized to the given projection parameters (distance between image and object) with the change of the grid’s geometric sizes and the inclination of the grid planes. An increased effect can be achieved if during the recording the grid is moving in the plane perpendicular to the projecting direction. Finding the best geometric parameters of the grid the divergence of the emitted beam by the x-ray tube should be taken into account as well.
The original document is available at http://549552.cz968.group/tiki-index.php?page=Elements+of+radiology+imaging