Introduction (introduction to: Monte Carlo Methods)

The dawn of the Monte Carlo methods are linked with the rise of nuclear, and by that to nuclear particle transport. This 'particle transport Monte Carlo' (from now on abbreviated simply to MC) can be viewed as the statistical equivalent of real transport process, a sort of simulation, that -using random numbers- particles travel one by one similarly to reality starting at the source ending their life (history) in an absorption or escape. MC can also be seen as a numerical integral evaluation technique where the particle transport equation in its integral form is taken as a Fredholm type (of II. kind) integral equation. This latter interpretation helps in formulating more efficient calculations then just mimicking nature, though this formalism breaks down at some processes often found in Medical Physics, like scintillation counting and coincidences.

Monte Carlo as a 'simulation of nature'

Following our first interpretation MC method is set of the following steps:

1. Following the distribution of the source but randomly selecting space, angle, energy and time coordinates
2. choosing a random free flight distance following in distribution the Beer-Lambert law, again
3. at the point of a collision based on the material properties and particle energy, random selection of an interaction type, then sampling randomly the outgoing coordinates following the distribution of the interaction in question
4. Repeating the 2nd and 3rd steps until the particle and its progeny gets absorbed or leaks out of the system

 
Every time the particle hits the detector a contribution is given to the detector counts usually determined by a (usually deterministic) detector function of the particle coordinates. The final MC result is the average of the contributions to the detector count.

Monte Carlo as a numerical integration tool

Let us take the following integral to calculate where D is a detector function and 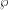is some probability density function (pdf), like the pdf of every possible interaction point of a particle throughout its life, or just a simple 1D pdf; and P accordingly a multidimensional -perhaps infinite dimensional- phase space variable.

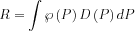
Let us take random samples following the pdf

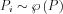
Now R can be estimated as:

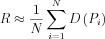
The expectation of this expression obviously assures that the estimator is unbiased.
The analog process is meant to give through the simulation of the particle life samples of this underlying pdf.

The next section is about how to sample pdf's.

 

---