Inverse Radon transfrom with Riesz potentials

The Fourier inversion formula simply lead us the filtering with |r| in the frequency domain and its alternative formulation with the differential and Hilbert transform operators. Using the Riesz potentials we can give a family of solutions where the Fourier inversion formula is just one of the members.

The 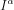$ I^{\alpha } Riesz-potential can be defined of a function of n-dimensions as follows:
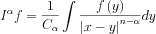
$ I^{\alpha }f=\frac{1}{C_{\alpha }}\int \frac{f\left ( y \right )}{\left | x-y \right |^{n-\alpha }}dy
Here 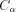$ C_{\alpha } is a constant. Similarly to the Hilbert transform we can give a definition using the Fourier transform:
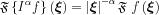
$ \mathfrak{F}\left \{ I^{\alpha } f \right \} \left ( \boldsymbol{\xi } \right )= \left | \boldsymbol{\xi } \right |^{-\alpha }\mathfrak{F}\ f \left ( \boldsymbol{\xi } \right )

Here 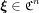$ \boldsymbol{\xi } \in \mathfrak{C}^{n}.
From this definition we can see
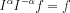
$ I^{\alpha }I^{-\alpha }f=f
Let us write the Riesz-potential of f with the Fourier definition:
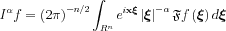
$ I^{\alpha }f=\left ( 2\pi \right )^{-n/2}\int_{R^{n}} e^{i\mathbf{x}\boldsymbol{\xi }}\left | \boldsymbol{\xi } \right |^{-\alpha }\mathfrak{F}f\left ( \boldsymbol{\xi } \right )d \boldsymbol{\xi }

Let us change variables to an n-dimensional polar coordinate system with notations:
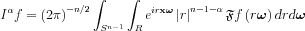
$ I^{\alpha }f=\left ( 2\pi \right )^{-n/2}\int_{S^{n-1}}\int_{R} e^{ir\mathbf{x}\boldsymbol{\omega }}\left | r \right |^{n-1-\alpha }\mathfrak{F}f\left ( r\boldsymbol{\omega } \right )drd\boldsymbol{\omega }
Let us fill in the result of the multidimensional Central Slice Theorem:
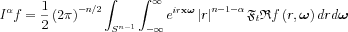
$ I^{\alpha }f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}\int_{S^{n-1}}\int_{-\infty }^{\infty} e^{ir\mathbf{x}\boldsymbol{\omega }}\left | r \right |^{n-1-\alpha }\mathfrak{F}_{t}\mathfrak{R}f\left ( r,\boldsymbol{\omega } \right )drd\boldsymbol{\omega }
With operator notations we can write:
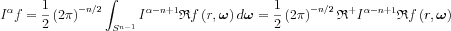
$ I^{\alpha }f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}\int_{S^{n-1}} I^{\alpha-n+1 }\mathfrak{R}f\left ( r,\boldsymbol{\omega } \right )d\boldsymbol{\omega }=\frac{1}{2}\left ( 2\pi \right )^{-n/2}\mathfrak{R}^{+} I^{\alpha-n+1 }\mathfrak{R}f\left ( r,\boldsymbol{\omega } \right )

On both sides calculating the $ I^{-\alpha } potentials:
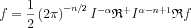
$ f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}I^{-\alpha }\mathfrak{R}^{+} I^{\alpha-n+1 }\mathfrak{R}f\left
and from that several inversion formulae can be obtained.

In the case of 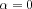$ \alpha=0 we get back the earlier shown inversion formula. It is worthwhile to highlight the case of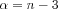$ \alpha=n-3 now
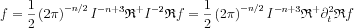
$ f=\frac{1}{2}\left ( 2\pi \right )^{-n/2}I^{-n+3 }\mathfrak{R}^{+} I^{-2}\mathfrak{R}f\left=\frac{1}{2}\left ( 2\pi \right )^{-n/2}I^{-n+3 }\mathfrak{R}^{+} \partial _{t}^{2}\mathfrak{R}f\left

which at least partially reinstates locality of the inversion formula.

 


The original document is available at http://549552.cz968.group/tiki-index.php?page=Inverse+Radon+transfrom+with+Riesz+potentials