Inverse transformation of the proper rational function

Let’s describe the denominator of proper rational function into fully-factored form:

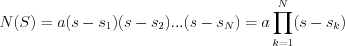
$$N(S) = a(s-s_{1})(s-s_{2})...(s-s_{N}) = a \prod_{k=1}^{N}(s-s_{k})$

If 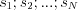$$s_{1};s_{2};...;s_{N}$ are single roots of 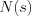$N(s) , then the partial fractions of 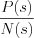$$\frac{P(s)}{N(s)}$ can be written as follow:

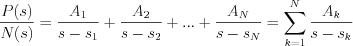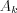$$\frac{P(s)}{N(s)} = \frac{A_{1}}{s-s_{1}} + \frac{A_{2}}{s-s_{2}} + ... + \frac{A_{N}}{s-s_{N}} = \sum_{k=1}^{N}\frac{A_{k}}{s-s_{k}}$ where $$A_{k}$ coefficients can be derived by the following expression:

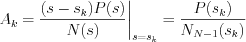
$$A_{k} = \frac{(s-s_{k})P(s)}{N(s)}\bigg{|}_{s=s_{k}} = \frac{P(s_{k})}{N_{N-1}(s_{k})}$

Consequently, the 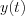$y(t) output response function can be derived, by the attenuation theorem of Laplace transformation for a 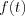$f(t) input function as follow:

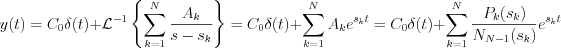
$$y(t) = C_{0} \delta (t) + \mathcal{L}^{-1}\left\{\sum_{k=1}^{N}\frac{A_{k}}{s-s_{k}}\right\} = C_{0} \delta (t) + \sum_{k=1}^{N}A_{k}e^{s_{k}t} = C_{0} \delta (t) + \sum_{k=1}^{N}}\frac{P_{k}(s_{k})}{N_{N-1}(s_{k})}e^{s_{k}t}$

Let’s see that case, when e.g. 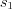$$s_{1}$ is multiple order pole (i.e. root). Let’s make the further assumption, 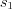$$s_{1}$ is M ordered pole of 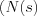$(N(s) . The partial fractions of 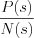$$\frac{P(s)}{N(s)}$ can be written in the following shape:

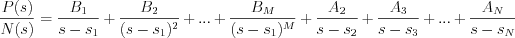
$$ \frac{P(s)}{N(s)}=\frac{B_1}{s-s_1}+\frac{B_2}{(s-s_1)^2}+\tex{...}+\frac{B_M}{(s-s_1)^M}+\frac{A_2}{s-s_2}+\frac{A_3}{s-s_3}+\tex{...}+\frac{A_N}{s-s_N}$

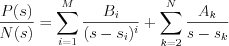
$$ \frac{P(s)}{N(s)}= \sum_{i=1}^{M}\frac{B_i}{(s-s_i)^i}+\sum_{k=2}^{N}\frac{A_k}{s-s_k}$

The output response function is as follow:
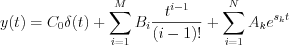$$ y(t)=C_0\delta(t)+ \sum_{i=1}^{M}B_i\frac{t^{i-1}}{(i-1)!}+ \sum_{i=1}^{N}A_ke^{s_kt}$ ,where $$ B_i=\frac{1}{(M-L)!}\frac{d^{M-i}}{ds^{M-i}} \left [ (s-s_1)^M\frac{P(s)}{N(s)} \right ]_{s=s_1}$ way is possible to derive.

The following Laplace transformation rule has been applied too
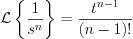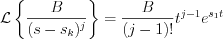
$$ \mathcal{L} \left \{ \frac{1}{s^n} \right \} = \frac{t^{n-1}}{(n-1)!}$ and $$ \mathcal{L} \left \{ \frac{B}{(s-s_k)^j} \right \} =\frac{B}{(j-1)!}t^{j-1}e^{s_1t}$

It is possible to conclude by the obtained result, if the system description operator "L" can be built up, by the knowledge of the internal structure of the constant coefficients linear invariant system (with the help of constant coefficients integral-differential equations), then the output response may be derived by the known input function with its initial conditions. The properties of the system can be characterized both in the extended complex frequency domain and in the real parameter space.

The original document is available at http://549552.cz968.group/tiki-index.php?page=Inverse+transformation+of+the+proper+rational+function