Linear Operators
Linear System Modeling by Linear Operators
Functioning of an imaging system with particular conditions can be described by the system description operator by abstract way. Consequently, it is practical to give a short summary about the properties of operators and enhance that operator set being well apply able in the model description on both imaging and image processing fields. One of the important condition is, the system description operators should be linear i.e. should map between the elements of linear space.
Definition:
Operator is a rule, mapping, transformation between the elements of set. Operator associates with the elements of same or other set by a prescribed transformation. In the following model description the mapping is in the linear space i.e. only those operator will be considered, which associates with the elements of the linear space.
Let 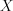 ,
,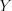 be subset of
be subset of 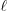 linear space i.e.
linear space i.e. 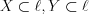 . Operator
. Operator  performs such an association between the
performs such an association between the 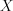 and
and 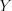 set, where
set, where 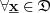 elements of
elements of 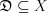 subset will be mapped the
subset will be mapped the  elements of
elements of 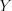 linear space. (Figure 4.).
linear space. (Figure 4.).
The 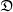 set is called the domain of the operator, while
set is called the domain of the operator, while 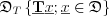 is the image of the operator.
is the image of the operator.
Definition: If the domain and the image of the  operator are in same linear space, then
operator are in same linear space, then  is the operator of
is the operator of 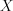 linear space.
linear space.
Definition: If the mapping of the elements of  subset by
subset by  operator results scalar value set as an image, i.e.
operator results scalar value set as an image, i.e. 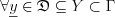 , where
, where  is the set of the real and complex numbers, then
is the set of the real and complex numbers, then
 is called linear functional.
is called linear functional.
Operation rules between the operators:
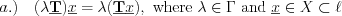
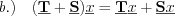
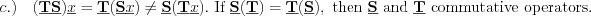
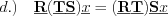
Definition  operator is bijective between the
operator is bijective between the 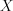 and
and 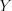 set, for
set, for 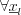 , and
, and 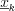 elements, where all the
elements, where all the 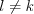 cases
cases 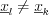 then
then 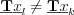 .
.
Definition Let  be a bijective operator. Consequently,
be a bijective operator. Consequently, 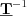 operator is the inverse of
operator is the inverse of  , if the domain of
, if the domain of 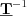 is the image of
is the image of  and
and 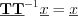 , in case of
, in case of  .
.
Linear Operators:
 is linear operator, if
is linear operator, if
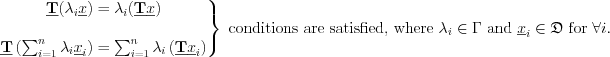
Linear operators are playing important role both in the abstract mathematical modeling and in the evaluation and description of the imaging systems. Imaging methods as well as the analysis of the time and space dependent processes (such as various bio-chemical processes and time dependent signal analysis) described by linear shift invariant operators are high priority modeling procedures. Denote the set of linear shift invariant operators 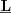 , where
, where  . The description of space and time dependent process can be expressed in the following way:
. The description of space and time dependent process can be expressed in the following way:
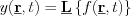
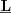 linear operator is shift invariant, if,
linear operator is shift invariant, if,
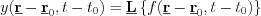
Time and space independent linear shift invariant systems can be described by linear shift invariant operators - 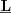 -. Systems described by
-. Systems described by 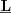 are called linear system by constant coefficients (where the coefficients represent the system parameters being time and space independent). If a running process in the linear shift invariant system is time independent, then the process equation is
are called linear system by constant coefficients (where the coefficients represent the system parameters being time and space independent). If a running process in the linear shift invariant system is time independent, then the process equation is 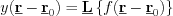 , if space independent, then
, if space independent, then 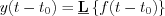 . The relation between the input and output variables will be described by single parameter (denoted by „
. The relation between the input and output variables will be described by single parameter (denoted by „ ”) way in the followings due to the more simple formulas (where „
”) way in the followings due to the more simple formulas (where „ ” may represent any variables - time, space coordinate, ….etc. -)(Figure 5.).
” may represent any variables - time, space coordinate, ….etc. -)(Figure 5.).
The relation between the input and output function can be described in the followings: 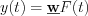 by system transfer way, or
by system transfer way, or 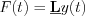 y(t) by the system description operators.
y(t) by the system description operators.
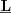 operator can be expressed for linear systems having constant coefficients as follow:
operator can be expressed for linear systems having constant coefficients as follow:
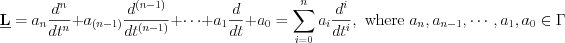
are the system parameters being independent of the „ ” variable (
” variable (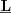 is invariant).
is invariant).
Consequently, the system description equation is: 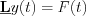
The output response i.e. the general solution of the equation can be derived by the followings: 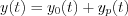 , where
, where 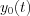 is the complementary function (it is the response of zero input, i.e. general solution of the homogenous equation), while
is the complementary function (it is the response of zero input, i.e. general solution of the homogenous equation), while 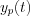 is the particular solution i.e. the response of the particular input function (i.e. exciting of the system) by the existing initial conditions.
is the particular solution i.e. the response of the particular input function (i.e. exciting of the system) by the existing initial conditions.
![$
\left.\begin{matrix}
\textbf{\underline{L}}y_{0}(t)=0\\
\\
\textbf{\underline{L}}y_{p}(t)=F(t)
\end{matrix}\right\}
\textbf{\underline{L}} \left[y_{0}(t)+y_{p}(t)\right] = F(t)](lib/equation/pictures/cda5f5704db85c5cc1ef6a630319c918.png)
In case of the system described by  : the complementary function -
: the complementary function - 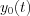 - gives the transient response of the system, while
- gives the transient response of the system, while 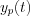 is the particular solution describing the stationary response (state) of the system by a particular input (exciting) function.
is the particular solution describing the stationary response (state) of the system by a particular input (exciting) function.
Let’s consider the following 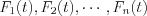 independent input functions of the
independent input functions of the 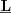 system operator, where the obtained responses are:
system operator, where the obtained responses are: 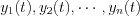 .
.
It is known:
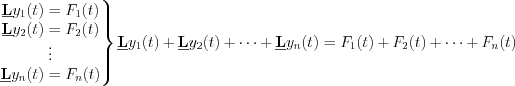
![$\textbf{\underline{L}}\left[\sum_{i=1}^{n}y_{i}(t) \right] = \sum_{i=1}^{n}F_{i}(t),](lib/equation/pictures/7a2ea6e3c75688a1ec43de4fcb3b707e.png) where the principle of superposition for linear systems have been derived.
where the principle of superposition for linear systems have been derived.
Linear invariant operators -L- physical phenomenon description
Let’s consider two simple physical examples showing on Figures 6. and 7. The system description linear invariant operator 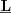 will be determined for both phenomenon in the followings:
will be determined for both phenomenon in the followings:
A mass „m” is mounted on a spring having „k” spring constant and 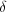 attenuation factor. F(t) is the excited force. Differential equation of mechanical model: attenuation factor. F(t) is the excited force. Differential equation of mechanical model: 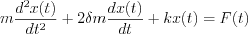 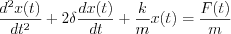 | „R” resistor, „C” capacitor and L inductivity are serial connected through „K” switch to U(t) excited input voltage. Differential equation of electric model: 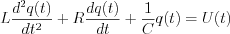 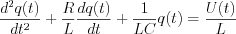 |
Apply the following denoting: 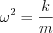 ; and
; and 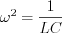
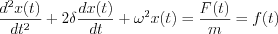 | 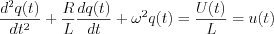 |
System description operators of both physical phenomenon are mathematically identical:
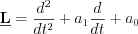 operator describes both physical phenomenon.
operator describes both physical phenomenon.
Operator of the mechanical model:
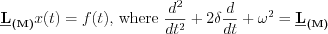
Operator of the electric circuit model:
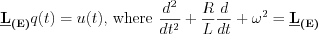
The two simple examples illustrate very well the determination of the system description operators by analytical way, as well as the system response analysis for different input functions. Unfortunately most of the cases the internal structures of the system are unknown. By means of the system responses obtained by various characteristic input functions is possible to make survey of the system properties and to create the system description operator by means of the obtained system responses. All of the methods and tools will be discussed in the following chapters.
The original document is available at http://549552.cz968.group/tiki-index.php?page=Linear+Operators