Linear shift invariant system description by the step response function


Applying of the step response function in order to characterize the property of the linear shift invariant system is a very often used method.

Definition: Output response of a linear shift invariant system by the Heavyside unit step function is called step response function:
Heavyside unit step function 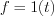$ f=1(t)
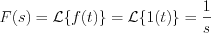
$ F(s) = \mathcal{L}\{f(t)\} = \mathcal{L}\{1(t)\} = \frac{1}{s}

Consequently the output response function:
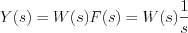
$ Y(s) = W(s)F(s) = W(s)\frac{1}{s}

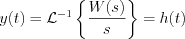$ y(t)=\mathcal{L}^{-1} \left\{\frac{W(s)}{s} \right\} = h(t) is called step response function.

It is possible to see, the relation between the step response function and the transfer function in the extended complex frequency domain is as follow:
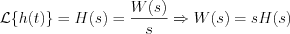$ \mathcal{L}\{h(t)\} = H(s) = \frac{W(s)}{s} \Rightarrow W(s)=sH(s), where the transfer function was derived by the step response function.

Furthermore, next question is arisen: step response function of a linear shift invariant system is known in the real parameter space. How is it possible to get the output response for $ f=f(t) general step function.

As it is known from previously:

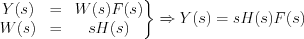
$ \left.\begin{matrix} Y(s)&=&W(s)F(s)\\ W(s)&=&sH(s) \end{matrix}\right\} \Rightarrow Y(s) = sH(s)F(s)

Let’s execute Laplace transformation of both sides:
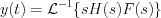
$ y(t)=\mathcal{L}^{-1}\{sH(s)F(s)\}

Apply the operation rules of Laplace transformation
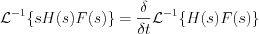
$ \mathcal{L}^{-1}\{sH(s)F(s)\} = \frac{\delta}{\delta t}\mathcal{L}^{-1}\{H(s)F(s)\}
,where 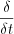$ \frac{\delta}{\delta t} is the weak derivative.

The output response function can be determined by the step response function as follow:

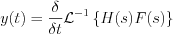
$ y(t)= \frac{\delta }{\delta t}\mathcal{L}^{-1}\left \{ H(s)F(s) \right \}
Apply the convolution rule for the product functions:

$ y(t)= \frac{\delta }{\delta t} \int_0f(\tau)h(t-\tau)d\tau= \frac{\delta }{\delta t} \left \[f(t)\ast h(t) \right \]

 
( by click here see the detailed driving)

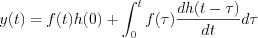$ y(t)=f(t)h(0)+\int_0^tf(\tau)\frac{dh(t-\tau)}{dt}d\tau , where 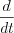$ \frac{d}{dt} means the regular derivative.

 
The output response determined by step response function is called Duhamel-theorem.


The original document is available at http://549552.cz968.group/tiki-index.php?page=Linear+shift+invariant+system+description+by+the+step+response+function