Nyírási elasztográfia

A nyírási elasztográfiai módszerek alapvetően abban különböznek a deformáció-mérésen alapuló módszerektől, hogy a vizsgált minta elasztikus paramétereit a bennük terjedő nyíráshullám sebességéből vezetjük le. A felhasznált összefüggés tehát, 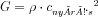$G=\rho\cdot {c_{nyírás}}^{2}$ , vagy összenyomhatatlan, homogén és izotróp anyagot feltételezve, 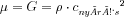$\mu=G=\rho\cdot {c_{nyírás}}^{2}$ . A nyíráshullám terjedését többnyire ultragyors képalkotási eljárásokkal követik nyomon. Mivel a nyírási modulus általában több nagyságrenddel kisebb a kompresszió modulusnál, ezért az ultrahang terjedési sebessége (emberi szövetekben átlagosan 1540 m/s) ténylegesen sokkal nagyobb a nyíráshullám sebességénél (ez körülbelül 10 m/s nagyságrendjébe esik), így a hullám terjedése valóban jól megfigyelhető ultrahang képalkotási eljárásokkal.
Nyírási hullámok terjedésének vizsgálata során azonban számolnunk kell azzal, hogy a legtöbb anyag elasztikus modulusai, így a nyírási modulus is erős frekvenciafüggést mutat. A kvázisztatikus elasztográfia leírásánál már felírtuk a mechanikai feszültségtenzor elemeire vonatkozó általános képletet: 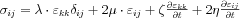$\sigma _{ij}=\lambda\cdot\varepsilon_{kk}\delta_{ij}+2\mu\cdot\varepsilon_{ij}+ \zeta\frac{\partial \varepsilon_{kk}}{\partial t}+2\eta\frac{\partial \varepsilon_{ij}}{\partial t}$ . Látható, hogy a feszültség értéke drasztikusan nő, ha a deformáció változási sebességét növeljük, vagyis nagyfrekvenciás nyíráshullámokhoz tartozó nyírási modulus, ami arányos a feszültséggel, igen nagy lehet a statikus esetben mért értékhez képest, ezt dinamikus modulusnak nevezzük.

Tranziens elasztográfia

A tranziens elasztográfiai módszerek nem időben állandósult hullámteret térképeznek fel, hanem rövid vibrációs gerjesztések hatására kialakuló tranziens nyíráshullám sebességét mérik meg valamilyen eljárással. A nyíróhullám létrehozására különféle gerjesztési eljárásokat alkalmaznak.
Ha valamilyen eddig ismertetett ultrahangos mérési eljárással megmérjük az elmozdulás-mezőt és annak időbeli alakulását a vizsgált térrészben, akkor a hullámegyenletből egyértelműen megkapható $\rho$ és $\mu$ értéke a minta minden pontjában, ha a határon $\mu$ ismert. Ugyanakkor a hullámegyenlet megoldása, lévén másodrendű parciális differenciálegyenlet, nagy numerikus hibát hordoz magában.
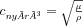A nyíráshullám sebességének meghatározásához nincs szükségünk $\rho$ és $\mu$ értékére külön-külön, hiszen a sebesség csak e két érték arányától függ: ${c_{nyíró}} =\sqrt \frac {\mu}{\rho}$ . Ez a hányados egy leszűkített adathalmaz, a terjedő hullám hullámfrontjának adataiból is meghatározható. A hullámfront adatainak meghatározásához célszerű definiálni az úgynevezett érkezési idő függvényt: 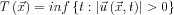$T\left(\vec{x} \right )=inf\left \{ t:\left | \vec{u}\left ( \vec{x},t \right ) \right | > 0\right \}$ , vagyis 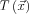$T\left(\vec{x} \right )$ az az időtartam, amíg a hullám az indítás helyétől az vec{x} pontba érkezik, ekkor a pontban mérhető elmozdulás először tér el a zérustól. 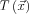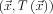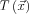A $T\left(\vec{x} \right )$ függvény ismeretében maga a hullámfront úgy definiálható, mint az $\left ( \vec{x},T\left(\vec{x} \right ) \right )$ pontok halmaza, ami valóban egy időben haladó felületet határoz meg, vagyis ha fix $\tau$ időpontban megrajzoljuk a kérdéses felületet, akkor magának a $T\left(\vec{x} \right )$ függvénynek a szintfelületeit kapjuk meg.
A hullámegyenlet: 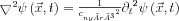$\bigtriangledown ^{2}\psi\left(\vec{x}, t \right )={\frac{1}{{c_{nyíró}}^{2}}} {\partial_{t} }^{2}\psi\left(\vec{x}, t \right )$ , ebbe a hullámfrontot beírva: 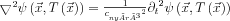$\bigtriangledown ^{2}\psi\left(\vec{x}, T\left(\vec{x} \right ) \right )={\frac{1}{{c_{nyíró}}^{2}}} {\partial_{t} }^{2}\psi\left(\vec{x}, T\left(\vec{x} \right ) \right )$ az egyenlőség nyilván továbbra is fennáll. A bal oldali Laplace-képzést láncszabály felhasználásával elvégezve:
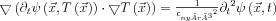
$\bigtriangledown \left (\partial_{t}\psi\left(\vec{x}, T\left(\vec{x} \right ) \right ) \cdot\bigtriangledown T\left(\vec{x} \right )\right )={\frac{1}{{c_{nyíró}}^{2}}} {\partial_{t} }^{2}\psi\left(\vec{x}, t \right )$
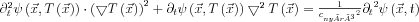
$\partial_{t}^{2}\psi\left(\vec{x}, T\left(\vec{x} \right )\right) \cdot\left (\bigtriangledown T\left(\vec{x} \right ) \right )^{2}+\partial_{t}\psi\left(\vec{x}, T\left(\vec{x} \right )\right)\bigtriangledown^{2} T\left(\vec{x} \right )={\frac{1}{{c_{nyíró}}^{2}}} {\partial_{t} }^{2}\psi\left(\vec{x}, t \right )$
Az egyenlet bal oldalán szereplő összeg második tagja minden esetben zérus, mivel 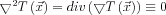$\bigtriangledown^{2} T\left(\vec{x} \right )=div\left (\bigtriangledown T\left(\vec{x} \right ) \right )\equiv 0$ . Ez könnyen belátható, hiszen az időben előrehaladó hullámfront minden pillanatban az érkezési idő függvény egy szintvonalának felel meg, vagyis a 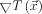$\bigtriangledown T\left(\vec{x} \right )$ vektor minden pontban merőleges a hullámfrontra, és annak haladási irányába mutat. Ebből már valóban következik, hogy az ilyen módon előállított vektormező egyetlen forrása maga a hullámforrás, vagyis valóban minden ezen kívül eső pontban 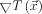$\bigtriangledown T\left(\vec{x} \right )$ divergenciája zérus.
Tehát a hullámfrontra felírt hullámegyenlet jelentősen egyszerűsíthető:
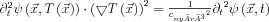
$\partial_{t}^{2}\psi\left(\vec{x}, T\left(\vec{x} \right )\right) \cdot\left (\bigtriangledown T\left(\vec{x} \right ) \right )^{2}={\frac{1}{{c_{nyíró}}^{2}}} {\partial_{t} }^{2}\psi\left(\vec{x}, t \right )$
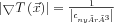
$\left |\bigtriangledown T\left(\vec{x} \right ) \right |={\frac{1}{\left |c_{nyíró} \right |}}$
Ez utóbbi alakot nevezzük a hullámfront terjedési sebességére vonatkozó eikonál-egyenletnek, ami már csak elsőrendű differenciálegyenlet, így megoldása lényegesen egyszerűbb, azonban problémaként felmerülhet, hogy olyan esetekben, ahol 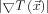$\left |\bigtriangledown T\left(\vec{x} \right ) \right |$ kicsi, a fordított arányosság miatt kis relatív hiba is nagy eltéréseket okozhat a terjedési sebesség értékében.
Látható, hogy a terjedési sebesség meghatározása általános többdimenziós esetben bár megoldható, de nehezen kivitelezhető nagy pontossággal. Emiatt az orvosi gyakorlatban a matematikailag is legkönnyebben kezelhető, egydimenziós tranziens elasztográfiai eljárás, a külső vibrációt alkalmazó, úgynevezett Fibroscan terjedt el. A készülék hepatológiai vizsgálatokra lett kifejlesztve, a máj elaszticitásának vizsgálatára, ami összefüggésben van a krónikus hepatitis, vagy egyéb májkárosító tényezők által okozott fibrózis mértékével. A készülék tehát elsősorban nagyobb térfogatú minta átlagos rugalmassági modulusának meghatározására alkalmas, nem kisméretű elváltozások felismerésére.

Vaszkuláris impulzushullám sebesség mérés

A vaszkuláris impulzushullám sebességének mérésén alapuló módszer lényege az, hogy külső rezgéskeltő eszköz, illetve akusztikus lökéshullám nélkül, egyszerűen a szervezetben amúgy is jelenlévő, artériás nyomásváltozások által keltett nyíráshullámok sebességét mérjük.
A vizsgálati eljárás nagy előnye, hogy a szokványos ultrahangfelvétel egészségügyi kockázatán túl nem hordoz semmilyen más veszélyt, hiszen a nyíráshullámokat nem külső eszközökkel keltjük. Hátránya ugyanakkor, hogy a természetes úton keltett elmozdulások gyakran kicsik, a lökések frekvenciája és ereje pedig kizárólag a szívműködéstől függ, így standardizálása nehézkes. Ennek ellenére kardiológiai és érvizsgálatokra, különös tekintettel az érfal rugalmasságának, és így az érelmeszesedés mértékének meghatározására a vaszkuláris impulzushullám sebesség mérés jól alkalmazható.

Nyíráshullám elasztográfia

Akusztikus lökéshullámokkal nem csak kis területre fókuszált elmozdulások hozhatók létre, hanem a fókuszfolt körül a lökés hatására nyíráshullám is indul. A keletkező nyíráshullám sebességéből az elasztikus modulusok meghatározhatóak. A nyíráshullám sebessége kiszámítható a tranziens elasztográfiánál ismertetett módon, keresztkorrelációval meghatározott elmozdulás adatokból.
Érdekes eljárás az úgynevezett szuperszonikus nyíráshullám elasztográfia. A módszer lényege, hogy nem egy fókuszált lökő nyalábot bocsátunk a vizsgált mintára, hanem egy egyenes mentén több lökést hozunk létre, olyan módon, hogy a nyíráshullám forrása mozog a mintán belül. Ha a lökéseket elég gyorsan generáljuk egymás után, akkor elérhető, hogy a forrás a közegben érvényes hullámterjedési sebességnél gyorsabban haladjon, így egy a hangrobbanáshoz hasonló jelenség játszódik le a mintában, a nyíráshullámok interferenciájából Mach-kúp alakul ki, ahogy ez a következő ábrán látható:

Szuperszonikus képalkotás elve

A Mach-kúp mentén, az ábrán is látható módon, nyírási síkhullámok alakulnak ki. A Mach-kúp nyílásszöge: 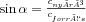$\sin\alpha=\frac{c_{nyíró}}{c_{forrás}}$ , így egyszerűen a nyílási szög méréséből megkaphatjuk a nyírási hullám sebességét, amiből a nyírási modulus és a Young-modulus megkapható.
A Young-modulus mérését ebben az eljárásban szögmérésre vezettük vissza, ezért a módszer az egydimenziós tranziens elasztográfiához hasonlóan alapvetően nagyobb térfogatú minta átlagos rugalmassági modulusának meghatározására alkalmas, így a Fibroscanhez hasonlóan például diffúz májbetegség (fibrózis) vizsgálható ezen eljárás segítségével.

Vibrációs és „csúszóhullám” elasztográfia

Vibrációs elasztográfiai módszerek időben harmonikus gerjesztést alkalmaznak, gyakran valamilyen külső vibrációkeltő eszköz segítségével. A kezdeti tranziens jelenségek lecsengése után a mintabeli elmozdulások a külső kényszer hatására szintén harmonikussá válnak, így ha a gerjesztés körfrekvenciája , akkor Newton második törvényének általános alakja:
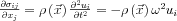
$\frac{\partial \sigma_{ij}}{\partial x_{j}}=\rho\left(\vec{x} \right )\frac{\partial^2 u_{i}}{\partial t^2}=-\rho\left(\vec{x} \right )\omega^{2}u_{i}$
$\partial_{i} p\left ( \vec{x} \right )+\partial_{i}\left [ \mu\left(\vec{x} \right ) \left ( \partial _{j} u_{i}+ \partial _{i} u_{j}\right )\right ]=-\rho\left(\vec{x} \right )\omega^2 u_{i}$

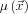A differenciálegyenlet az elmozdulás adatok ismeretében megoldható $\mu\left(\vec{x} \right )$ -re és $p\left(\vec{x} \right 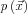)$ -re, és a módszer nagy előnye, hogy $\omega$ ismeretében az idő szerinti második deriválás egyszerű szorzással kiváltható, így az időszerinti numerikus deriválás okozta hiba kiküszöbölhető. Nagy hibát okozhat azonban a térszerinti deriválás numerikus elvégzése, emiatt számos egyéb numerikus eljárás

Ha például a mintát teljesen összenyomhatatlannak tekintjük, akkor benne a nyomás mindenhol a külső nyomásértékkel azonos lesz, így deriváltja zérus. Az egyenlet így:
$\partial_{i}\left [ \mu\left(\vec{x} \right ) \left ( \partial _{j} u_{i}+ \partial _{i} u_{j}\right )\right ]=-\rho\left(\vec{x} \right )\omega^2 u_{i}$
Amennyiben azt is feltehetjük, hogy a nyírási modulus, vagyis 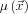$\mu\left(\vec{x} \right )$ csak kis mértékben változik, akkor a 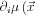$\partial_{i}\mu\left(\vec{x}$ -vel szorzott tag elhagyható, vagyis a leegyszerűsített egyenlet Helmholtz-típusú lesz:
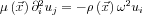
$\mu\left(\vec{x} \right )\partial _{i}^2 u_{j}=-\rho\left(\vec{x} \right )\omega^2 u_{i}$
Látható, hogy a fenti egyenlet elmozdulás vektor egyes komponenseire felírt hullámegyenlet, melyből a terjedési sebesség a már ismert képlet: 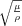$\sqrt {\frac{\mu}{\rho}}$ . A nyíráshullám alakja itt azonban biztosan harmonikus lesz a külső kényszer miatt, így a terjedési sebesség adott frekvencia mellett például a hullámhossz mérésével megkapható: 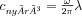${c_{nyíró}}=\frac{\omega}{2\pi}\lambda$ . A hullámhossz pedig az ismert elmozdulás adatokból könnyen kiszámítható, ily módon a differenciálegyenlet megoldása elkerülhető. A képalkotás felbontása a hullámhossz méretével egy nagyságrendbe esik, így kellően nagy frekvencia mellett jelentősen csökkenthető. Ugyanakkor számításba kell vennünk, hogy a nagyfrekvenciás nyíráshullámok behatolási mélysége relatíve kicsi.

t fejlesztettek ki a probléma megoldására.

Az úgynevezett csúszóhullám elasztográfiai eljárás a vibrációs elasztográfiai módszer módosított változata, ami nagyon hasonlít a vibroakusztográfiás módszerhez. Két harmonikus nyíráshullám interferenciájából kialakul az összeg és a különbség frekvenciával rendelkező harmonikus hullám is. Ha a két külső rezgéskeltő frekvenciájának eltérése kicsi, akkor a keletkező alacsonyfrekvenciás hullám hullámhossza olyan nagy lesz, hogy a hullám egyszerű B-módú ultrahang segítségével, szemmel is követhető, ugyanakkor a megnövekedett hullámhossz miatt csak rossz felbontás érhető el.

The original document is available at http://549552.cz968.group/tiki-index.php?page=Ny%C3%ADr%C3%A1si+elasztogr%C3%A1fia