Példa a kvázisztatikus elasztográfia egyenletrendszerének numerikus megoldására

Bizonyos határfeltételek mellett milyen, a következő, viszonylag jól programozható eljárással ismerhetjük meg az elasztikus modulus értékét a szövetekben.
Tételezzük fel, hogy a vizsgált szövet belsejében valamilyen jól körülhatárolt inhomogenitás található. Ebben az esetben a Young-modulus, és így $\mu$ értéke nem folytonos függvénye a helynek, hanem az adott inhomogenitás határán véges szakadással rendelkezik. Egy valódi vizsgálat, például rákos daganat keresése esetén jó közelítéssel teljesül ez a feltétel, és egy ilyen mérés során a feladat nem csupán a tumor Young-modulusának meghatározása, hanem pontos helyének és alakjának feltérképezése is.
Tehát a legtöbb valódi esetben a fenti négy egyenlet mellett adott határfeltételünk a következő: egyensúlyban az inhomogenitás határán a mechanikai feszültség felületre normális része azonos kell legyen a határon belül és kívül. Azaz: 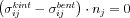$\left ( \sigma_{ij}^{kint}-\sigma_{ij}^{bent} \right )\cdot n_{j}=0$ , ahol 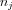$n_{j}$ a határfelület egységnyi hosszúságú normálvektora a határ valamely pontjában. Behelyettesítve a feszültségtenzor már megismert egyszerűsített alakját: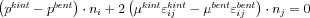 $\left ( p^{kint}-p^{bent} \right )\cdot n_{i}+2\left ( \mu^{kint}\varepsilon_{ij}^{kint}-\mu^{bent}\varepsilon_{ij}^{bent}\right )\cdot n_{j}=0$
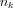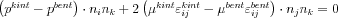Mivel ebben a levezetésben a nyomás értékéről semmilyen feltételezéssel nem élünk, ezért az imént összevont alakban felírt (i=1,2,3 esetén) három egyenletből álló egyenletrendszerből azt ki kell ejtenünk. Ha a fenti alakot beszorozzuk $n_{k}$ -val: $\left ( p^{kint}-p^{bent} \right )\cdot n_{i} n_{k}+2\left ( \mu^{kint}\varepsilon_{ij}^{kint}-\mu^{bent}\varepsilon_{ij}^{bent}\right )\cdot n_{j} n_{k}=0$ . Könnyen belátható, hogy a j-re való összegzést elvégezve, például i=1 és k=2 esetén a nyomást tartalmazó tagok azonosak lesznek az i=2 k=1 indexekkel felírt egyenletbeli tagokkal, így a két egyenletből már kiejthetők: 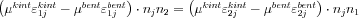$\left ( \mu^{kint}\varepsilon_{1j}^{kint}-\mu^{bent}\varepsilon_{1j}^{bent}\right )\cdot n_{j} n_{2}=\left ( \mu^{kint}\varepsilon_{2j}^{kint}-\mu^{bent}\varepsilon_{2j}^{bent}\right )\cdot n_{j} n_{1}$ , hasonlóan nyerhető egy független egyenlet az 1-3 indexpár felhasználásával. Az egyenletrendszer tehát:
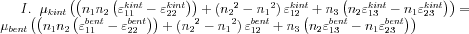
$I.\;\; \mu_{kint}\left( \left ( n_{1}n_{2}\left ( \varepsilon_{11}^{kint}-\varepsilon_{22}^{kint} \right ) \right )+\left ( {n_{2}}^{2}-{n_{1}}^{2} \right )\varepsilon_{12}^{kint}+n_{3}\left(n_{2}\varepsilon_{13}^{kint}-n_{1}\varepsilon_{23}^{kint}\right)\right )=\mu_{bent}\left( \left ( n_{1}n_{2}\left ( \varepsilon_{11}^{bent}-\varepsilon_{22}^{bent} \right ) \right )+\left ( {n_{2}}^{2}-{n_{1}}^{2} \right )\varepsilon_{12}^{bent}+n_{3}\left(n_{2}\varepsilon_{13}^{bent}-n_{1}\varepsilon_{23}^{bent}\right)\right )$
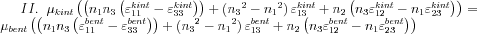
$II.\;\; \mu_{kint}\left( \left ( n_{1}n_{3}\left ( \varepsilon_{11}^{kint}-\varepsilon_{33}^{kint} \right ) \right )+\left ( {n_{3}}^{2}-{n_{1}}^{2} \right )\varepsilon_{13}^{kint}+n_{2}\left(n_{3}\varepsilon_{12}^{kint}-n_{1}\varepsilon_{23}^{kint}\right)\right )=\mu_{bent}\left( \left ( n_{1}n_{3}\left ( \varepsilon_{11}^{bent}-\varepsilon_{33}^{bent} \right ) \right )+\left ( {n_{3}}^{2}-{n_{1}}^{2} \right )\varepsilon_{13}^{bent}+n_{2}\left(n_{3}\varepsilon_{12}^{bent}-n_{1}\varepsilon_{23}^{bent}\right)\right )$
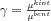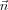Látható, hogy ha ismertnek feltételezzük a deformációtenzor elemeinek értékét, akkor a fenti egyenletekben csupán a felületre merőleges egységvektor komponensei, illetve a $\gamma=\frac{\mu^{kint}}{\mu^{bent}}$ arány ismeretlen. Nyilvánvaló, hogy homogén anyagot vizsgálva a $\gamma$ hányados értéke tetszőleges $\vec{n}$ irány esetén egy, mivel $\mu$ homogén esetben konstans. Ugyanúgy, ha $\mu$ folytonosan, és a mérésünk felbontásához képest kellően lassan változik, a hányados értéke továbbra is egy marad. 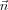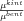Azonban egy határbeli pontban nézve tetszőleges irányítású $\vec{n}$ esetén a $\gamma$ -ra kapott érték jelentősen eltér egytől, bár csak a valódi normálvektor komponensekkel számítva egyezik meg $\frac{\mu^{kint}}{\mu^{bent}}$ pontos értékével.
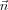Ezt a tulajdonságot felhasználva a fenti egyenletrendszer $\gamma$ -ra numerikusan megoldható két lépésben: először tetszőleges $\vec{n}$ irányokkal végigpásztázzuk a mintát, így a 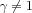$\gamma\neq 1$ feltételből megkapjuk a határ pontjainak koordinátáit, majd második lépésben a határ alakjának és helyének ismeretében már valóban a vizsgált felületre merőleges egységvektorok koordinátáival kiszámíthatjuk az egyes pontokban $\gamma$ értékét.
Természetesen az itt ismertetett eljáráson kívül számos más módszert is leírtak már a négy egyenletes differenciálegyenlet-rendszer és határfeltételeinek kielégítésére, azonban mivel az egyenletek egzakt megoldása nem lehetséges, minden ismert eljárás óriási számítástechnikai kapacitást igényel, mégis meglehetősen nagy hibával terhelt.

The original document is available at http://549552.cz968.group/tiki-index.php?page=P%C3%A9lda+a+kv%C3%A1zisztatikus+elasztogr%C3%A1fia+egyenletrendszer%C3%A9nek+numerikus+megold%C3%A1s%C3%A1ra