Response function in general case

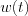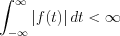The following description shows, how is possible to give a system response for a general input function (non-step function) by a linear invariant system having $ w(t) weight function and under the condition: $$ \int_{-\infty}^{\infty} \left | f(t) \right |dt <\infty$ .

Let’s consider the next two figures:

Let’s approximate the 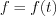$ f=f(t) function by the series of such Dirac-impulses, where
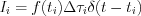$$ I_i=f(t_i)\Delta\tau_i\delta(t-t_i)$ , for $$ t \in \left [ t_i;t_{i+1} \right ]$

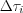Let $$ \Delta\tau_i$ infinitesimal small, i.e. 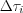$$ \Delta\tau_i$ represents much more smaller value comparing to the corresponded system characteristic parameter value. The system response according to the approximated input impulse with the known weighted function can be expressed as follow:

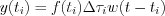
$$ y(t_i)=f(t_i)\Delta\tau_iw(t-t_i)$

Let’s determine the following limit in order to get the response function for the complete real parameter domain:

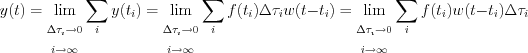
$$ y(t)=\lim_{ \begin{matrix} _{\Delta\tau_i \to 0} \\ _{i \to \infty } \end{matrix}} \sum_{i}y(t_i)=\lim_{ \begin{matrix} _{\Delta\tau_i \to 0} \\ _{i \to \infty } \end{matrix}} \sum_{i}f(t_i)\Delta \tau _iw(t-t_i)=\lim_{ \begin{matrix} _{\Delta\tau_i \to 0} \\ _{i \to \infty } \end{matrix}} \sum_{i}f(t_i)w(t-t_i)\Delta \tau _i$

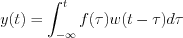
$$ y(t)=\int_{-\infty}^tf(\tau)w(t-\tau)d\tau$

Return to the ‘Transfer Characteristic’ chapter

The original document is available at http://549552.cz968.group/tiki-index.php?page=Response+function+in+general+case