S11.


Solution:

The partial differential equation can be written by expressing the Laplace operator as follow:
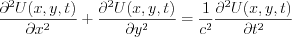
$ \frac{\partial^2 U(x,y,t)}{\partial x^2}+\frac{\partial^2 U(x,y,t)}{\partial y^2}= \frac{1}{c^2}\frac{\partial^2 U(x,y,t) }{\partial t^2}

 
Let’s apply the Fourier transformation first by x and then y.
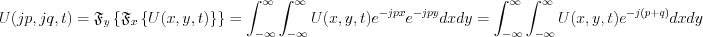
$ U(jp,jq,t)= \mathfrak{F}_y\left \{ \mathfrak{F}_x \left \{ U(x,y,t) \right \} \right \} = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} U(x,y,t)e^{-jpx} e^{-jpy}dxdy = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} U(x,y,t)e^{-j(p+q)}dxdy

It is known from the Fourier transformation rules:
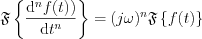
$ \mathfrak{F}\left \{ \frac{\mathrm{d}^n f(t))}{\mathrm{d} t^n} \right \}=(j\omega)^n\mathfrak{F}\left \{ f(t) \right \}

Let’s execute Fourier transformation on both side of partial differential equation:
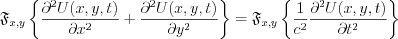
$ \mathfrak{F}_{x,y} \left \{ \frac{\partial^2 U(x,y,t)}{\partial x^2}+\frac{\partial^2 U(x,y,t)}{\partial y^2} \right \} = \mathfrak{F}_{x,y} \left \{ \frac{1}{c^2}\frac{\partial^2 U(x,y,t) }{\partial t^2} \right \}

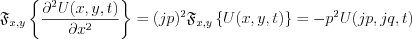
$ \mathfrak{F}_{x,y} \left \{ \frac{\partial^2 U(x,y,t)}{\partial x^2} \right \} =(jp)^2 \mathfrak{F}_{x,y} \left \{ U(x,y,t) \right \} =-p^2U(jp,jq,t)

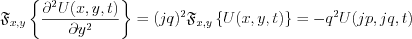
$ \mathfrak{F}_{x,y} \left \{ \frac{\partial^2 U(x,y,t)}{\partial y^2} \right \} =(jq)^2 \mathfrak{F}_{x,y} \left \{ U(x,y,t) \right \} =-q^2U(jp,jq,t)

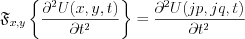
$ \mathfrak{F}_{x,y} \left \{ \frac{\partial^2 U(x,y,t)}{\partial t^2} \right \} = \frac{\partial^2 U(jp,jq,t)}{\partial t^2}

The second ordered partial differential equation has been transformed to second order linear differential equation with constant coefficient.
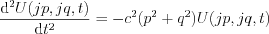
$ \frac{\mathrm{d}^2 U(jp,jq,t) }{\mathrm{d} t^2} = -c^2(p^2+q^2)U(jp,jq,t)

It is known, the solution of that differential equation is:
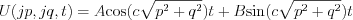$ U(jp,jq,t)= A\text{cos}(c\sqrt{p^2+q^2})t + B\text{sin}(c\sqrt{p^2+q^2})t like harmonic oscillator.

Let’s use the available initial condition in Fourier frequency space:
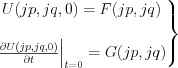
$ \left.\begin{matrix} U(jp,jq,0)= F(jp,jq) \\ \\ \left.\begin{matrix} \frac{\partial U(jp,jq,0) }{\partial t} \end{matrix}\right|_{t=0}=G(jp,jq) \end{matrix}\right\}

Consequently:
$ \frac{\partial U(jp,jq,0) }{\partial t}= \frac{\partial }{\partial t} \left [A\text{cos}(c\sqrt{p^2+q^2}t) + B\text{sin}(c\sqrt{p^2+q^2}t) \right ]_{t=0}=G(jp,jq)

$ \left [-Ac\sqrt{p^2+q^2}\text{sin}(c\sqrt{p^2+q^2}t)+ B c\sqrt{p^2+q^2}\text{cos}(c\sqrt{p^2+q^2})t \right ]_{t=0}=G(jp,jq)

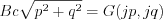
$ Bc\sqrt{p^2+q^2}=G(jp,jq)

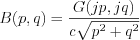
$ B(p,q)=\frac{G(jp,jq)}{ c\sqrt{p^2+q^2}}

$ \left.\begin{matrix} U(jp,jq,t) \end{matrix}\right|_{t=0}=F(jp,jq)= \left.\begin{matrix} \left [ A\text{cos}(c\sqrt{p^2+q^2})t + B\text{sin}(c\sqrt{p^2+q^2})t \right ] \end{matrix}\right|_{t=0}

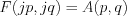
$ F(jp,jq)=A(p,q)

Consequently 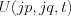$ U(jp,jq,t) is expressed by the initial condition in frequency space (i.e. by Fourier transformed expression):

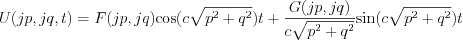
$ U(jp,jq,t)=F(jp,jq) \text{cos}(c\sqrt{p^2+q^2})t + \frac{G(jp,jq)}{ c\sqrt{p^2+q^2}} \text{sin}(c\sqrt{p^2+q^2})t

Then 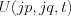$ U(jp,jq,t) can be obtained by the p and q variables inverse Fourier transformation
$ u(x,y,t).

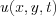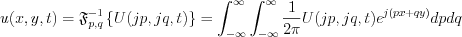
$ u(x,y,t)= \mathfrak{F}_{p,q}^{-1}\left \{ U(jp,jq,t) \right \} = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \frac{1}{2\pi}U(jp,jq,t)e^{j(px+qy)}dpdq

$ U(x,y,t)= \frac{1}{2\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \left [F(jp,jq) \text{cos}(c\sqrt{p^2+q^2})t + \frac{G(jp,jq)}{ c\sqrt{p^2+q^2}} \text{sin}(c\sqrt{p^2+q^2})t \right ]dpdq

 
(Return to the Problems)


The original document is available at http://549552.cz968.group/tiki-index.php?page=S11.