S2.


Solution:
Let’s attempt to derive the Laplace transformation of 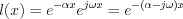$l(x)=e^{-\alpha x}e^{j\omega x}=e^{-(\alpha-j\omega)x} function instead of $f(x).

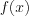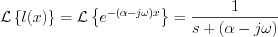$ \mathcal{L}\left\{l(x)\right\} = \mathcal{L}\left\{e^{-(\alpha-j\omega )x}\right\} = \frac{1}{s+(\alpha-j\omega)}; as it is known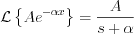 $\mathcal{L}\left\{Ae^{-\alpha x}\right\} = \frac{A}{s+\alpha}

Then, let’s make the following operations!

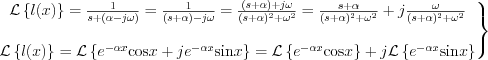
$ \left.\begin{matrix} \mathcal{L}\left\{l(x)\right\} = \frac{1}{s+(\alpha-j\omega)} = \frac{1}{(s+\alpha)-j\omega} = \frac{(s+\alpha)+j\omega}{(s+\alpha)^{2}+\omega^{2}} = \frac{s+\alpha}{(s+\alpha)^{2}+\omega^{2}}+j\frac{\omega}{(s+\alpha)^{2}+\omega^{2}}\\ \\ \mathcal{L}\left\{l(x)\right\} = \mathcal{L}\left\{e^{-\alpha x}\text{cos}x+je^{-\alpha x}\text{sin}x\right\} = \mathcal{L}\left\{e^{-\alpha x}\text{cos}x\right\} + j\mathcal{L}\left\{e^{-\alpha x}\text{sin}x\right\} \end{matrix}\right\}

Consequently the obtained results:
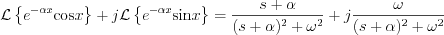
$ \mathcal{L}\left\{e^{-\alpha x}\text{cos}x\right\} + j\mathcal{L}\left\{e^{-\alpha x}\text{sin}x \right\} = \frac{s+\alpha}{(s+\alpha)^{2}+\omega^{2}}+j\frac{\omega}{(s+\alpha)^{2}+\omega^{2}}

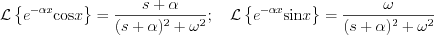
$ \mathcal{L}\left\{e^{-\alpha x}\text{cos}x\right\} = \frac{s+\alpha}{(s+\alpha)^{2}+\omega^{2}}; \quad \mathcal{L}\left\{e^{-\alpha x}\text{sin}x \right\} = \frac{\omega}{(s+\alpha)^{2}+\omega^{2}}

 
(Return to the Problems)


The original document is available at http://549552.cz968.group/tiki-index.php?page=S2.