S3.


Solution:

Let’s start to write the F(s) function by the following way:

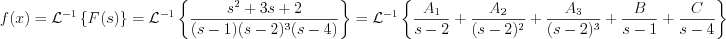
$ f(x)=\mathcal{L}^{-1}\left\{F(s)\right\} = \mathcal{L}^{-1}\left\{\frac{s^{2}+3s+2}{(s-1)(s-2)^{3}(s-4)}\right\} = \mathcal{L}^{-1}\left\{\frac{A_{1}}{s-2}+\frac{A_{2}}{(s-2)^{2}}+\frac{A_{3}}{(s-2)^{3}}+\frac{B}{s-1}+\frac{C}{s-4}\right\}

Let’s execute the partial fraction operation as follow!

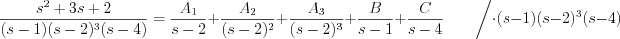
$ \frac{s^{2}+3s+2}{(s-1)(s-2)^{3}(s-4)}= \frac{A_{1}}{s-2}+\frac{A_{2}}{(s-2)^{2}}+\frac{A_{3}}{(s-2)^{3}}+\frac{B}{s-1}+\frac{C}{s-4} \quad \quad \bigg{/}\cdot(s-1)(s-2)^{3}(s-4)

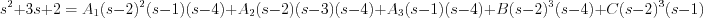
$ s^{2}+3s+2 = A_{1}(s-2)^{2}(s-1)(s-4) + A_{2}(s-2)(s-3)(s-4) + A_{3}(s-1)(s-4) + B(s-2)^{3}(s-4) + C(s-2)^{3}(s-1)

Let's substitute in the equation 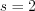$s=2 value! Parameter 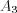$A_3 will be then determined.

 
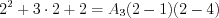
$2^{2}+3\cdot 2+2 = A_{3}(2-1)(2-4)

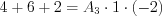
$4+6+2 = A_{3}\cdot 1\cdot (-2)

$A_{3}=-6

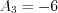
Next step: let’s substitute 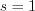$s=1 into the same equation for obtaining parameter $B:

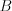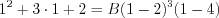
$1^{2}+3\cdot 1+2=B(1-2)^{3}(1-4)

$6 = B(-1)(-3)

$B=2

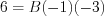
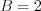
Let’s substitute 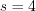$s=4 into the same equation in order to get parameter $C!

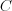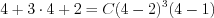
$4+3\cdot 4+2 = C(4-2)^{3}(4-1)

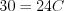
$30=24C

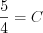
$\frac{5}{4}=C

Let’s write A3, B and C into the equation

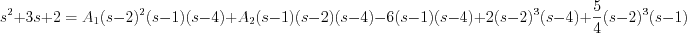
$s^{2}+3s+2 = A_{1}(s-2)^{2}(s-1)(s-4)+A_{2}(s-1)(s-2)(s-4) - 6(s-1)(s-4)+2(s-2)^{3}(s-4)+\frac{5}{4}(s-2)^{3}(s-1)

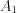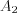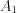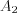where only $A_{1} and $A_{2} are unknown. $A_{1} and $A_{2} will be determined by the following way. First 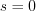$s=0, then 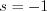$s=-1 will be substituted in the equation obtaining the following set of two linear equations for 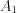$A_{1} and $A_{2}.

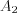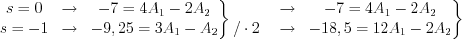
$ \left.\begin{matrix} s=0 & \to & -7 = 4A_{1}-2A_{2}\\ s=-1 & \to & -9,25 = 3A_{1}-A_{2} \end{matrix}\right\} \begin{matrix} \\ /\cdot 2 \end{matrix} \left.\begin{matrix} \quad \rightarrow & -7=4A_{1}-2A_{2}\\ \quad \rightarrow & -18,5 = 12A_{1}-2A_{2} \end{matrix}\right\}

Let’ substitute the two equation : 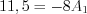$11,5 = -8A_{1}

Consequently 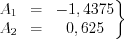$ \left.\begin{matrix} A_{1} & = & -1,4375\\ A_{2} & = & 0,625 \end{matrix}\right\}

Now all the coefficients of the partial fraction are known, and Laplace transformation can be executed.

 
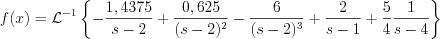
$f(x)=\mathcal{L}^{-1}\left\{-\frac{1,4375}{s-2}+\frac{0,625}{(s-2)^{2}}-\frac{6}{(s-2)^{3}}+\frac{2}{s-1}+\frac{5}{4} \frac{1}{s-4}\right\}

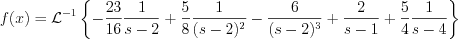
$f(x)=\mathcal{L}^{-1}\left\{-\frac{23}{16}\frac{1}{s-2}+\frac{5}{8}\frac{1}{(s-2)^{2}}-\frac{6}{(s-2)^{3}}+\frac{2}{s-1}+\frac{5}{4} \frac{1}{s-4}\right\}

$f(x)=\left[-\frac{23}{16}e^{2x}+\frac{5}{8}xe^{2x}-\frac{6}{2!}x^{2}e^{2x}+2e^{x}+\frac{5}{4}e^{4x}\right]1(x)

$f(x)=\left[2e^{x}+\frac{5}{4}e^{4x}+\frac{5}{8}xe^{2x}-3x^{2}e^{2x}-\frac{23}{16}e^{2x}\right]

 
(Return to the Problems)


The original document is available at http://549552.cz968.group/tiki-index.php?page=S3.