Sampling

The most programming languages offer a (pseudo)random number generator that gives samples of a uniform distribution in the range of (0,1).

A common MC sampling technique is the inverse cumulative method that using the uniformly sampled r random number produces a sample of the pdf:
$$ x_{i}=\left [\int_{-\infty}^{ X}\wp \left ( x \right )dx \right ]^{-1}\left ( r \right )$
We will see an example to this in the next section.

A lot simpler, but a lot less effective method is when we chose a pdf $ q that we can easily be sampled (it can simply be the uniform distribution and r is automatically a sample of it). Now let us write the integral like this:
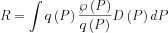
$$ R=\int q\left ( P \right ) \frac{\wp\left ( P \right )}{q\left ( P \right )} D\left ( P \right )dP$
let us choose P_i from q our estimate should be:
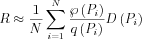
$$ R\approx \frac{1}{N}\sum_{i=1}^{N}\frac{\wp\left ( P_{i} \right )}{q\left ( P_{i} \right )}D\left (P_{i} \right )$
The new quantity arising is 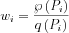$$ w_{i} = \frac{\wp\left ( P_{i} \right )}{q\left ( P_{i} \right )}$ the weight of the particle.

The next section shows the sampling of the free flight distance.

The original document is available at http://549552.cz968.group/tiki-index.php?page=Sampling