Sampling the free flight distance

According to the Beer-Lamber law the particle free flight follows an exponential distribution with the following pdf:
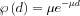
$$ \wp\left ( d \right )=\mu e^{-\mu d}$
A $$ \mu$ where the attenuation coefficient (total macroscopic cross section) values can be taken e.g. from here here.

Let us sample this using the inverse cumulative method:
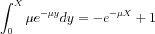
$$ \int_{0}^{X}\mu e^{-\mu y}dy= -e^{-\mu X}+1$

Let us equate this to the on (0,1) Uniformly distributed r random number:
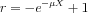
$$ r= -e^{-\mu X}+1$
After reordering and using the fact that the r random number is uniformly distributed on (0,1) therefore in distribution equals to 1-r:
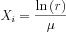
$$X_{i}=\frac{\ln \left (r \right )}{\mu }$

In heterogenous material distribution this sampling must be done for each homogenous subdomain separately.

After the flee flight we discuss interaction sampling.

The original document is available at http://549552.cz968.group/tiki-index.php?page=Sampling+the+free+flight+distance