The Hilbert-transform

The Hilbert transform

Though it's use is frequent in signal processing, it does have a significance in understanding tomographic image reconstruction, the Hilbert transform.
. The 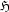$$ \mathfrak{H}$ Hilbert transform is defined as:
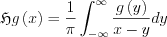
$$\mathfrak{H}g\left (x \right )=\frac{1}{\pi}\int_{-\infty }^{\infty }\frac{g\left ( y\right )}{x-y}dy$

The definition looks simple, to evaluate the integral looks a lot harder as the denominator harbours a singularity. It means we have to take the integral in a Cauchy principal value, so
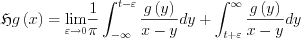
$$ \mathfrak{H}g\left ( x \right )=\underset{\varepsilon \rightarrow 0}{\lim} \frac{1}{\pi}\int_{-\infty }^{t-\varepsilon }\frac{g\left ( y \right )}{x-y}dy+\int_{t+\varepsilon }^{\infty }\frac{g\left ( y \right )}{x-y}dy$
Existence of such a limit can easily imagined, as for function g=1 the function 1/x can be integrated in Principa Value, being odd the result is 0, since the range of the integral is symmetric.

To ease the evaluation of the integral

note that the Hilbet transfrom is a convolution with function 1/x
Fourier transform then inverse Fourier transform the expression

$$\mathfrak{H}g\left ( x \right )=g\left ( x \right )*\frac{1}{\pi x}=\mathfrak{F}^{^{-1}}\mathfrak{F}\left \{ g\left ( x \right )*\frac{1}{\pi x} \right \}=\mathfrak{F}^{^{-1}}\left \{ \mathfrak{F}\left [ g\left ( x \right ) \right ] \mathfrak{F}\left [ \frac{1}{\pi x} \right]\right \}$
Let us evaluate the Fourier transform of 1/x:
$$\mathfrak{F}\left [ \frac{1}{x} \right ]=-\frac{1}{\pi}\int_{-\infty }^{\infty }\frac{e^{-i k x}}{x}dx=-\frac{1}{\pi}\int_{-\infty }^{\infty }\frac{\cos( kx)-i\sin\left ( kx \right )}{x}dx$

The function cos is even, divided by the odd "x" function the first term is again zero.
We have the next two terms remaining:
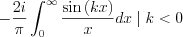
$$ -\frac{2i}{\pi}\int_{0}^{\infty }\frac{\sin\left ( kx \right )}{x}dx \mid k< 0$
and
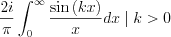
$$ \frac{2i}{\pi}\int_{0}^{\infty }\frac{\sin\left ( kx \right )}{x}dx \mid k>0$

Since
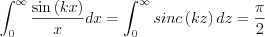
$$ \int_{0}^{\infty }\frac{\sin\left ( kx \right )}{x}dx=\int_{0 }^{\infty }sinc\left ( kz \right )}dz=\frac{\pi}{2}$

The result is, then:

$$\mathfrak{F}\left [ \frac{1}{x} \right ]=i sgn(k)$
where sgn is the sign function.
$$\mathfrak{H}g\left ( x \right )=\mathfrak{F}^{^{-1}}\left \{ \mathfrak{F}\left [ g\left ( x \right ) \right ] i sgn(k)\right \}$

This result, regarding the numerical evaluation technique is a lot simpler then the application of the basic definition, since the digital Fourier transform and its implementation technique (FFT) is a routinely applied, accessible and fast.

Our results also shows, that if we apply the Hilbert transform twice on the same function we obtain:
$$\mathfrak{H}\mathfrak{H}g\left ( x \right )=\mathfrak{F}^{^{-1}}\left [\left \mathfrak{F}[\mathfrak{F}^{^{-1}}\left \{ \mathfrak{F}\left [ g\left ( x \right ) \right ] i sgn(k)\right \} \right ]i sgn(k) \right ]=-g\left ( x \right )$

thus the inverse of the Hilbert-transfrom is -apart from a sign- is itself.
As an illustration we have prepared the 2D Hilbert transform of an image:

The original document is available at http://549552.cz968.group/tiki-index.php?page=The+Hilbert-transform