The Radon Transform in multiple dimensions

The Radon transform in 2D means an integral taken along a parametrized 2D linear set (normally a straight line). In multiple dimensions a linear geometrical set can mean a line or a hyperplane, the latter leads us to the multi-D generalization of our previous definition of the Radon-transform, the former gives the Ray (or X-ray) transform.

Radon transform in multiple dimensions

Let us take the paramters 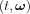$ \left(t,\boldsymbol{\omega} \right ) to describe a hyperplane (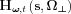$\mathbf{H}_{\boldsymbol{\omega},t}\left ( \mathbf{s},\boldsymbol{\Omega_{\perp} } \right )), where according to the its y points the integrals are taken, 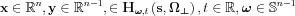$\mathbf{x}\in \mathbb{R}^{n},\mathbf{y}\in \mathbb{R}^{n-1},\in \mathbf{H}_{\boldsymbol{\omega},t}\left ( \mathbf{s},\boldsymbol{\Omega_{\perp} } \right ), t\in \mathbb{R} , \boldsymbol{\omega}\in \mathbb{S}^{n-1}), with that we have the definition of the Radon transform for an n dimensional function:
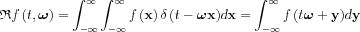
$ \mathfrak{R}f\left ( t,\boldsymbol{\omega} \right )=\int_{-\infty }^{\infty }\int_{-\infty }^{\infty } { f\left ( \mathbf{x} \right )\delta \left ( t-\boldsymbol{\omega} \mathbf{x} \right )}d\mathbf{x}= \int_{-\infty }^{\infty } { f\left ( t\boldsymbol{\omega}+ \mathbf{y} \right )}d\mathbf{y}

Ray-transform

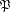If carry out the integral with regards to t, i.e. instead of a hyperplane we have a direction $ \boldsymbol{\omega} and along that we do a line integration, we obtain the other possible generalization of the 2D Radon transform, called the (X-)Ray transform. With the definitions above the $ \mathfrak{P} Ray transform is defined as:
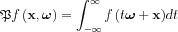
$ \mathfrak{P}f\left ( \mathbf{x},\boldsymbol{\omega} \right )= \int_{-\infty }^{\infty } { f\left ( t\boldsymbol{\omega}+ \mathbf{x} \right )}dt

where it is enough to take the values of x from a plane perpendicular to vector $ \boldsymbol{\omega}.

With these definitions we can construct the inverse of the Radon and the Ray transforms.


The original document is available at http://549552.cz968.group/tiki-index.php?page=The+Radon+Transform+in+multiple+dimensions