The sinogram
The sinogram
The 2D Radon transform is usually graphically represented as a sinogram, which means the intensity values 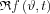 in the coordinate system of variables
in the coordinate system of variables 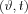 .
.
To understand the sinogram ( the result of a Radon transform) let us investigate the sinogram of a point and a line.
The Radon transform of a point
Let us take a point with coordinates (x0,y0). With that:
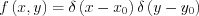
Thus
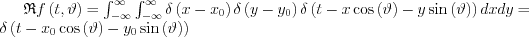
|
|
|
The result is nonzero only in points, where
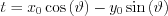
Now the result obtained -as the Radon transform of a point- resembles a sine, this is why the graph representation of the Radon transform of variables 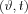 is called a sinogram.
is called a sinogram.
Radon transform of a line
Now let us take a line and use the usual parametrization of offset and angle and choose some fixed values for them of 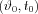 . In the (x,y) space the expression describing this line is:
. In the (x,y) space the expression describing this line is:
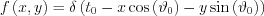
Now let us take its Radon transform:
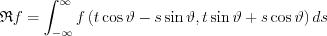
substituting
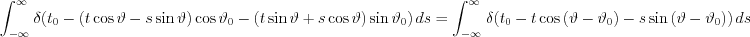
Taking the coefficient of s:
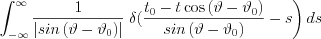
if the result of the expression 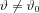 is
is
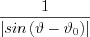
that results in a bounded result as it does not contain singularity.
If  holds then a Dirac delta is independent of the s integration variable:
holds then a Dirac delta is independent of the s integration variable:
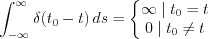
Finally we obtain nonzero results at the point of 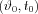 on the sinogram, apart from the finite part.
on the sinogram, apart from the finite part.
|
|
|
General sinograms
Interpreting a sinogram is not an easy task, as a starting point, based on the above, points of a sinogram may correspond to lines. Usually, the more recognizable features are sinusoids that belong to compact structures in the (x,y) space.
Now we show some random examples .
Non-centered disk:
|
|
|
Non-centered square:
|
|
|
Shepp-Logan head phanstom:
|
|
|
Picture of a foal:
|
|
|
In the next section we discuss the general properties of the Radon transform.
The original document is available at http://549552.cz968.group/tiki-index.php?page=The+sinogram