The sinogram

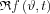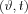The 2D Radon transform is usually graphically represented as a sinogram, which means the intensity values $\mathfrak{R}f\left ( \vartheta,t \right )$ in the coordinate system of variables $$\left ( \vartheta,t \right )}$ .

To understand the sinogram ( the result of a Radon transform) let us investigate the sinogram of a point and a line.

The Radon transform of a point

Let us take a point with coordinates (x₀,y₀). With that:

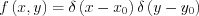
$$ f\left ( x,y)=\delta \left ( x-x_{0} \right )\delta \left ( y-y_{0} \right )$
Thus
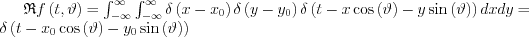
$\mathfrak{R}f\left ( t,\vartheta \right )=\int_{-\infty }^{\infty}\int_{-\infty }^{\infty}\delta \left ( x-x_{0} \right )\delta \left ( y-y_{0} \right ) \delta \left ( t-x\cos \left (\vartheta \right )-y\sin \left ( \vartheta\right )\right )dxdy= \delta \left ( t-x_{0}\cos \left (\vartheta \right )-y_{0}\sin \left ( \vartheta\right )\right )$

Pointin the (x,y) space	Point in the sinogram space

The result is nonzero only in points, where

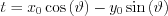
$$t=x_{0}\cos \left (\vartheta \right )-y_{0}\sin \left ( \vartheta\right )$

Now the result obtained -as the Radon transform of a point- resembles a sine, this is why the graph representation of the Radon transform of variables 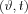$$\left ( \vartheta,t \right )}$ is called a sinogram.

Radon transform of a line

Now let us take a line and use the usual parametrization of offset and angle and choose some fixed values for them of 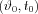$$\left ( \vartheta_{0},t_{0} \right )$ . In the (x,y) space the expression describing this line is:

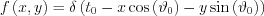
$$ f\left ( x,y \right )=\delta \left ( t_{0}-x\cos \left (\vartheta_{0} \right )-y\sin \left ( \vartheta_{0}\right )\right )$
Now let us take its Radon transform:

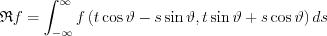
$$\mathfrak{R}f=\int_{-\infty }^{\infty }f\left ( t\cos \vartheta -s\sin \vartheta ,t\sin \vartheta +s\cos \vartheta \right )ds$
substituting
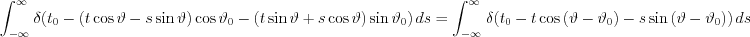
$$\int_{-\infty }^{\infty }\left \delta (t_{0}- \left (t\cos \vartheta -s\sin \vartheta \right )\cos \vartheta _{0} -\left (t\sin \vartheta +s\cos \vartheta \right )\sin \vartheta _{0} \right ) ds= \int_{-\infty }^{\infty }\left \delta (t_{0}- t\cos\left ( \vartheta -\vartheta_{0} \right ) -s\sin \left (\vartheta-\vartheta_{0} \right ) \right ) ds$
Taking the coefficient of s:
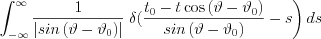
$$ \int_{-\infty }^{\infty }\frac{1}{\left | sin \left (\vartheta-\vartheta_{0} \right ) \right |} \left \delta (\frac{t_{0}- t\cos\left ( \vartheta -\vartheta_{0} \right )}{sin \left (\vartheta-\vartheta_{0} \right )} -s \right ) ds$

if the result of the expression 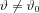$$\vartheta\neq \vartheta_{0}$ is
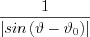
$$ \frac{1}{\left | sin \left (\vartheta-\vartheta_{0} \right ) \right |}$
that results in a bounded result as it does not contain singularity.
If $$\vartheta= \vartheta_{0}$ holds then a Dirac delta is independent of the s integration variable:

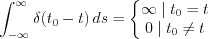
$$ \int_{-\infty }^{\infty }\left \delta (t_{0}- t \right ) ds =\left\{\begin{matrix} \infty \mid t_{0}=t\\ 0 \mid t_{0}\neq t \end{matrix}\right.$

Finally we obtain nonzero results at the point of 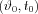$$\left ( \vartheta_{0},t_{0} \right )$ on the sinogram, apart from the finite part.

line in the (x,y) spacen	Radon transform of a line (approximate)

General sinograms

Interpreting a sinogram is not an easy task, as a starting point, based on the above, points of a sinogram may correspond to lines. Usually, the more recognizable features are sinusoids that belong to compact structures in the (x,y) space.

Now we show some random examples .

Non-centered disk:

image in the (x,y) space	Sinogram (Radon transform) X-axis: angle, Y axis: paramtere t

Non-centered square:

image in the (x,y) space	Sinogram (Radon transform) X-axis: angle, Y axis: paramtere t

Shepp-Logan head phanstom:

image in the (x,y) space	Sinogram (Radon transform) X-axis: angle, Y axis: paramtere t

Picture of a foal:

image of a foal	Radon transform of the picture of a foal

In the next section we discuss the general properties of the Radon transform.

The original document is available at http://549552.cz968.group/tiki-index.php?page=The+sinogram