Theory and basic laws of sampling

Those mathematical tools and procedures have been written in the previous chapters – discussion of linear system properties – to be applied for describing and characterizing of the shift invariant quantized i.e. discretized system in the followings. Operation of quantization is not a linear transformation. It is a mapping from the continuous space described by continuous values into the discrete set to be characterized by integer numbers. Basic laws and consequences of the quantization process is described in the current chapter by one dimension approach. Parameter value denoted by 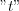represents time in the current description, i.e. the quantization process will be discussed by the time dependent events (but 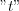may represent other “so called” general parameters /i.e. domain set/ too completely similar way as were mentioned before. That case the applied formalism and discussion is fully analogue.

Relations between the analogue and digital information evaluation process

It is possible to see in Figure 33., that the data processing unit determines the various typical parameters of the process taking place in a system. Characteristic parameters of the system process can be evaluated in an analogue way too, avoiding the quantization operations /as was written and mentioned in the previous chapters/ .
The 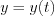$y=y(t) signal can only be digitaly processed after the quantization of the 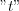parameter domain as well as the discretization of its corresponded value set i.e. both set are converted into digital values.

Figure 33.

Consequently, the digitization of 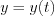$y=y(t) happen by the subsequent two steps:
a) Quantization of 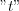, i.e. quantization of the parameter domain
b) Quantization of 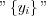, i.e. discretization of the corresponded value set (codomain).

Definitions:
a) Quantize of the domain value, i.e. 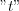time values - as the independent variables - is called Sampling, or more precisely Sampling & Hold (S&H).

b) Discretization unit executes the quantization of the amplitude i.e. the corresponded value set (codomain 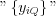) is called Analogue to Digital Conversion denoting ADC or A/D.

Sampling-unit:
Sampling converts the continuous time and amplitude signal - i.e. both domain and codomain are represented by real values - into continuous amplitude signal series set (codomain remains continuous real value) but quantized time (i.e. domain set is represented by integer numbers). 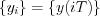$$\{y_{i}\}=\{y(iT)\}$ , where 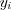$$y_{i}$ is equivalent with the corresponded real value at 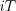$iT discrete moment of the process, where “i” is natural number (see Figure 34.). 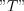is called sampling time (or “aperture window” in abstract way).

Figure 34.

Quantizing Unit:
Quantizing unit converts the continuous amplitude signal - i.e. real value codomain - to discrete signal set (discrete “integer” codomain). Consequently the quantization is a non-linear operation having the following description:
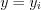$$y=y_{i}$ , for $$x_{i} < x < x_{i+1}, \quad i = 1,2,\cdots,N$ , where “i” is natural number and N represents the number of sampling. are the elements of the discretized, integer value codomain i.e. output, while is the input of the quantizing unit (see Figure 35.)

Figure 35.

“y” is the output of quantizing unit
“x” is the input of quantizing unit

Consequently, the analogue 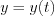$y=y(t) signal series will be presented by finite integer numbers. Next step is the analysis of the nature of the sampled and quantized process in order to obtain
consequences between the analogue and digital signal evaluations.

Sampling law

Let’s investigate the relation between the particular represented sample and its Fourier transformation (see Figure 36. and 37.)

Figure 36.

Figure 37.

Fourier transformation of the signal is as follow: 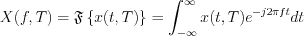$${X(f,T)=\mathfrak{F}\left \{ x(t,T) \right \}=\int_{-\infty }^{\infty }x(t,T)e^{-j2{\pi}ft}dt}$

Let’s repeat the 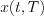$x(t,T) signal periodically in the 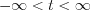$$-\infty<t<\infty$ domain.

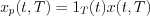$x_p(t,T)=1_T(t)x(t,T) series of this periodic function exists and can be written as follow:

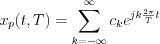$$x_p(t,T)=\sum_{k=-\infty}^{\infty}c_ke^{jk\frac{2\pi}{T}t}$ , where the coefficients of Fourier series can be determined: 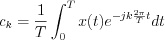$$c_k=\frac{1}{T}\int_{0}^{T}x(t)e^{-jk\frac{2\pi}{T}t}dt$ , i.e. set of 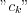will determine injectively the 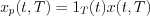$x_p(t,T)=1_T(t)x(t,T) periodic function.

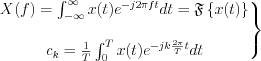$$\left.\begin{matrix} X(f)=\int_{-\infty}^{\infty}x(t)e^{-j2{\pi}ft}dt=\mathfrak{F}\left \{ x(t) \right \} \\ \\ c_k=\frac{1}{T}\int_{0}^{T}x(t)e^{-jk\frac{2\pi}{T}t}dt \end{matrix}\right\}$ . It is possible to conclude: 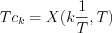$$Tc_k=X(k\frac{1}{T},T)$ which means, if 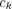$$c_{k}$ Fourier coefficients are known, then values of Fourier spectrum of 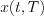$x(t,T) function at the 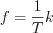$$f=\frac{1}{T}k$ points can be derived. These values consequently will determine the values of 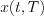$x(t,T) function at every moment.

First law of sampling:

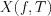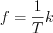Fourier transformation of signals being finite in time i.e. $X(f,T) function are determined by the values at every points, where $$f = \frac{1}{T}k$ .

Let’s consider the following band limited spectrum (see Figure 38.), where the bandwidth is 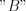in the Fourier spectrum.

Figure 38.

It cam be stated that the 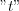dependent signal, function can be derived by the above shown band limited spectrum:

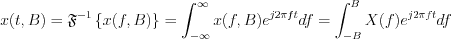
$$x(t,B)=\mathfrak{F}^{-1}\left \{ x(f,B) \right \}=\int_{-\infty}^{\infty}x(f,B)e^{j2{\pi}ft}df=\int_{-B}^{B}X(f)e^{j2{\pi}ft}df$

Let’s repeat the 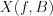$X(f,B) function by 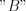periodicity in the whole 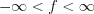$$-\infty<f<\infty$ frequency domain by similar way as was described above in time domain case.

Thus 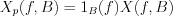$X_p(f,B)=1_B(f)X(f,B) .

Fourier series of the periodic signal in frequency domain:
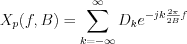$$X_p(f,B)=\sum_{k=-\infty}^{\infty}D_ke^{-jk\frac{2{\pi}}{2B}f}$ , where the 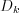$D_k coefficients are

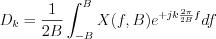
$$D_k=\frac{1}{2B}\int_{-B}^{B}X(f,B)e^{+jk\frac{2{\pi}}{2B}f}df$

Consequently,
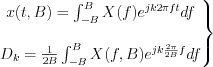$$\left.\begin{matrix} x(t,B)=\int_{-B}^{B}X(f)e^{jk2{\pi}ft}df \\ \\ D_k=\frac{1}{2B}\int_{-B}^{B}X(f,B)e^{jk\frac{2{\pi}}{2B}f}df \end{matrix}\right\}$ , where it is obtained: 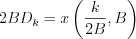$$2BD_k=x\left(\frac{k}{2B},B\right)$ i.e. the set of 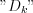will determine the 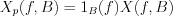$X_p(f,B)=1_B(f)X(f,B) periodic function. Furthermore, it is possible to see, that 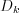$$D_{k}$ coefficients determine the value of 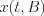$x(t,B) function at 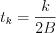$$t_k=\frac{k}{2B}$ each 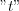moment. Since all the existing 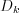$$D_{k}$ coefficients will determine 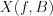$X(f,B) function, then they will determine also 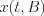$x(t,B) function by similar way as was used previously (i.e. 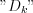coefficients will determine 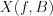$X(f,B) function everywhere, consequently 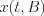$x(t,B) is also determined in every 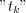points).

Second law of sampling:

The time domain (or the generalized 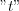parameter domain) questions and problems will be under consideration by the second law of sampling. The main interpretation of the second law of sampling is the signal (function) determining by a 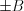$$\pm B$ band limited spectrum with the values at 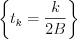$$\left\{t_k=\frac{k}{2B}\right\}$ points.

Let’s see, how is possible to get from the sampled values the 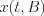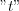$x(t,B) dependent function.

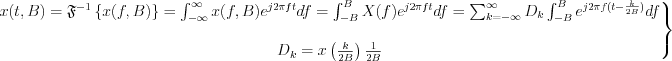
$$\left.\begin{matrix} x(t,B)=\mathfrak{F}^{-1}\left \{ x(f,B) \right \}=\int_{-\infty}^{\infty}x(f,B)e^{j2{\pi}ft}df=\int_{-B}^{B}X(f)e^{j2{\pi}ft}df=\sum_{k=-\infty}^{\infty}D_k\int_{-B}^{B}e^{j2{\pi}f(t-\frac{k}{2B})}df\\ \\ D_k=x\left(\frac{k}{2B}\right)\frac{1}{2B} \end{matrix}\right\}$

Thus:
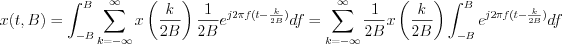
$$x(t,B)=\int_{-B}^{B}\sum_{k=-\infty}^{\infty}x \left (\frac{k}{2B}\right) \frac{1}{2B}e^{j2{\pi}f(t-\frac{k}{2B})}df=\sum_{k=-\infty}^{\infty}\frac{1}{2B}x\left (\frac{k}{2B}\right)\int_{-B}^{B}e^{j2{\pi}f(t-\frac{k}{2B})}df$

Let’s determine the 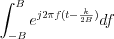$$\int_{-B}^{B}e^{j2{\pi}f(t-\frac{k}{2B})}df$ integral:

$$\int_{-B}^{B}e^{j2{\pi}f(t-\frac{k}{2B})}df=\frac{1}{j2\pi(t-\frac{k}{2B})}\left [ e^{j2{\pi}f(t-\frac{k}{2B})} \right ]_{-B}^B=\frac{1}{\pi(t-\frac{k}{2B})}\frac{e^{j2{\pi}B(t-\frac{k}{2B})}-e^{-j2{\pi}B(t-\frac{k}{2B})}}{2j}$

i.e.

$$\int_{-B}^{B}e^{j2{\pi}f(t-\frac{k}{2B})}df=\frac{ \text{sin}\left [ 2{\pi}B(t-\frac{k}{2B}) \right ]}{{\pi}(t-\frac{k}{2B})}=2B\frac{ \text{sin}\left [ 2{\pi}B(t-\frac{k}{2B}) \right ]}{2{\pi}B(t-\frac{k}{2B})}$

Let’s execute the necessary substitution:

$$x(t,B)=\sum_{k=-\infty}^{\infty}x \left (\frac{k}{2B} \right )\frac{1}{2B}2B\frac{ \text{sin}\left [ 2{\pi}B(t-\frac{k}{2B}) \right ]}{2{\pi}B(t-\frac{k}{2B})}$

$$x(t,B)=\sum_{k=-\infty}^{\infty}x\left (\frac{k}{2B}\right )\frac{ \text{sin}\left [ 2{\pi}B(t-\frac{k}{2B}) \right ]}{2{\pi}B(t-\frac{k}{2B})}$

Mathematical interpretation of the second law of sampling is the following:

Any of the finite band limited and Fourier transformable 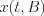$x(t,B) signal (or function) can be expandable into series on the $$ \left \{ \frac{ \text{sin}\left [ 2{\pi}B(t-\frac{k}{2B}) \right ]}{2{\pi}B(t-\frac{k}{2B})} \right \}$ function set and the coefficient of element 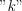of the 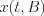$x(t,B) function will be the value of 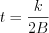$$ t=\frac{k}{2B}$ point.

Mathematical interpretation of the first law of sampling:

Similar steps and methods have to apply as above. Result of the expanding into series in the frequency domain of the 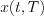$x(t,T) signal (or function) with 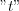time width (or parameter width) will be the following:

$$X(f,T)=\sum_{k=-\infty}^{\infty}X(\frac{k}{T})\frac{ \text{sin}\left [ {\pi}T(f-\frac{k}{T}) \right ]}{{\pi}T(t-\frac{k}{T})}$ , where the coefficient of the the element 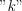of the series is the value of 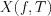$X(f,T) at the 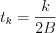$$ t_k=\frac{k}{2B}$ point.

Physical interpretation of the sampling laws:

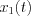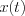Main goal of the physical interpretation is to clarify the relation between the $x_1(t) and $x(t) functions, where 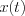$x(t) is the input function, while 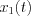$x_1(t) is the sampled process (signal or function) of S&H. Let’s consider Figure 39., 40., 41 and 42.

Figure 39. Input function of sampling-unit undergoing to sampling

Figure 40.	Figure 41.
Simple switching diagram of the ideal sampling-unit , where 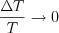$$\frac{\Delta T}{T} \rightarrow 0$

Figure 42. Sampled process depending on the time

The sampled process can be expressed in the 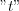domain as follow: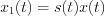 $x_1(t)=s(t)x(t)

Let’s execute the Fourier transformation on both sides:
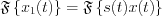
$$\mathfrak{F} \left\{x_1 (t) \right\}= \mathfrak{F}\left\{s(t)x(t)\right\}$

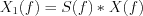$$X_{1}(f)=S(f) \ast X(f)$ , where 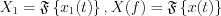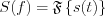$$X_{1}=\mathfrak{F}\left \{x_{1}(t)\right \}, X(f)=\mathfrak{F}\left \{x(t)\right \}$ , $$S(f)=\mathfrak{F}\left \{s(t)\right \}$ is a convolution in the frequency domain. Since $s(t) switching function is a periodic function, the Fourier function of $s(t) can be derived on the following way:

Let’s apply the main properties of Dirac-delta:

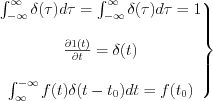
$$ \left.\begin{matrix} \int^{\infty}_{-\infty} \delta(\tau) d\tau = \int_{-\infty}^{\infty} \delta(\tau) d\tau = 1\\ \\ \frac{\partial1(t)}{\partial t}=\delta(t)\\ \\ \int_{\infty}^{-\infty}f(t)\delta(t-t_{0})dt=f(t_{0}) \end{matrix}\right\}$

If an 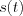$s(t) function is periodic, then the Fourier series can be written as follow:
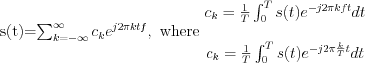
$$ $s(t)=\sum_{k=-\infty}^{\infty}c_{k}e^{j2\pi ktf}, \text{ where } \begin{matrix} c_{k}=\frac{1}{T} \int_{0}^{T}s(t)e^{-j2\pi kft}dt\\ \\ c_{k}=\frac{1}{T} \int_{0}^{T}s(t)e^{-j2\pi \frac{k}{T}t}dt \end{matrix}$

Consequently, the Fourier transformation of an periodic 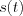$s(t) function is:

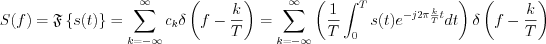
$$ S(f)=\mathfrak{F}\left \{s(t)\right \}=\sum_{k=-\infty}^{\infty}c_{k}\delta\left (f-\frac{k}{T}\right )=\sum_{k=-\infty}^{\infty}\left (\frac{1}{T}\int_{0}^{T}s(t)e^{-j2\pi \frac{k}{T}t}dt\right)\delta\left(f-\frac{k}{T}\right)$

Thus the Fourier transformation of the 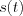$s(t) switching function can be written by means of Fourier series, where the 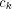$c_k coefficient is derived as the following:

$$ c_{k}=\frac{1}{T}\int_{\Theta-\frac{\Delta T}{2}}^{\Theta+\frac{\Delta T}{2}}1e^{-j2\pi k\frac{1}{T}t}dt=\frac{1}{T}\int_{\Theta-\frac{\Delta T}{2}}^{\Theta+\frac{\Delta T}{2}}e^{-j2\pi \frac{k}{T}t}=\frac{1}{T}\text{ } \frac{1}{-j2\pi \frac{k}{T}}\left [ e^{-j2\pi \frac{k}{T}t} \right ]_{\Theta-\frac{\Delta T}{2}}^{\Theta+\frac{\Delta T}{2}}$

$$ c_{k}=\frac{1}{T}\text{ } \frac{1}{-j2\pi \frac{k}{T}}\left [ e^{-j2\pi \frac{k}{T}(\Theta + \frac{\Delta T}{2})} - e^{-j2\pi \frac{k}{T}(\Theta - \frac{\Delta T}{2})} \right ]=\frac{1}{T}\text{ } \frac{1}{\pi \frac{k}{T}}\text{ }e^{-j2\pi \frac{k}{T}\Theta} \left [ \frac{e^{-j2\pi \frac{k}{T}\frac{\Delta T}{2}}-e^{j2\pi \frac{k}{T}\frac{\Delta T}{2}}}{-2j} \right ]$

$$ c_{k}=e^{-j2\pi \frac{k}{T}\Theta}\text{ } \frac{\Delta T}{T} \text{ }\frac{1}{\Delta T \pi \frac{k}{T}} \left [\frac{e^{j\pi \frac{k}{T}\Delta T}-e^{-j\pi \frac{k}{T}\Delta T}}{2j} \right ] = e^{-j2\pi \frac{k}{T}\Theta}\text{ } \frac{\Delta T}{T} \text{ }\frac{ \text{sin}\pi \frac{k}{T} \Delta T}{\pi \frac{k}{T}\Delta T}$

Consequently, Fourier series of 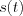$s(t) switching function: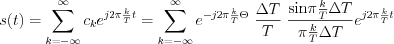 $$s(t)=\sum_{k=-\infty}^{\infty}c_{k}e^{j2\pi \frac{k}{T}t}=\sum_{k=-\infty}^{\infty}e^{-j2\pi \frac{k}{T}\Theta}\text{ } \frac{\Delta T}{T} \text{ }\frac{ \text{sin}\pi \frac{k}{T} \Delta T}{\pi \frac{k}{T}\Delta T} e^{j2\pi\frac{k}{T}t}$

The Fourier transformation of the 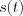s(t) switching function based on chapter 2.6.4:
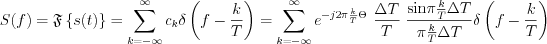
$$ S(f)=\mathfrak{F}\left \{ s(t) \right \} =\sum_{k=-\infty}^{\infty}c_{k}\delta \left(f-\frac{k}{T}\right)=\sum_{k=-\infty}^{\infty}e^{-j2\pi\frac{k}{T}\Theta}\text{ }\frac{\Delta T}{T}\text{ }\frac{ \text{sin}\pi \frac{k}{T}\Delta T}{\pi \frac{k}{T}\Delta T} \delta\left(f-\frac{k}{T}\right)$

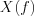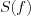Let’s write down the sample process in the frequency domain (by the Fourier transformation) by substituting $X(f) and $S(f) formula and applying the convolution rule:
$$ X_{1}(f)=X(f)\ast S(f) = \int_{-\infty}^{\infty}X(\nu)S(f-\nu)d\nu = \int_{-\infty}^{\infty}X(\nu) \sum_{k=-\infty}^{\infty}e^{-j2\pi \frac{k}{T}\Theta}\text{ }\frac{\Delta T}{T}\text{ }\frac{ \text{sin}\pi \frac{k}{T} \Delta T}{\pi \frac{k}{T} \Delta T} \delta \left [ \left(f- \frac{k}{T} \right)-\nu \right]d\nu$

$$ X_{1}(f) = \sum_{k=-\infty}^{\infty}e^{-j2\pi \frac{k}{T}\Theta}\text{ }\frac{\Delta T}{T}\text{ }\frac{ \text{sin}\pi \frac{k}{T} \Delta T}{\pi \frac{k}{T} \Delta T} \int_{-\infty}^{\infty}X(\nu) \delta \left [ \left(f- \frac{k}{T} \right)-\nu \right]d\nu = \sum_{k=-\infty}^{\infty}e^{-j2\pi \frac{k}{T} \Theta}\text{ }\frac{\Delta T}{T}\text{ }\frac{ \text{sin}\pi \frac{k}{T} \Delta T}{\pi \frac{k}{T} \Delta T} X\left(f-\frac{k}{T}\right)$

Let’s see, what conclusions are possible to do by the obtained expression: 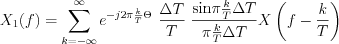$$X_{1}(f) = \sum_{k=-\infty}^{\infty} e^{-j2 \pi \frac{k}{T} \Theta}\text{ }\frac{\Delta T}{T}\text{ }\frac{ \text{sin}\pi \frac{k}{T} \Delta T}{\pi \frac{k}{T} \Delta T} X\left(f-\frac{k}{T}\right)$

1.) Fourier transformation of the sampled signal may be obtained by the 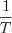$$\frac{1}{T}$ weighted periodic recurrence of the spectrum of input signal among the frequency axis (see Figure 43.).

Figure 43.

2.) If the model of sampling is an “Ideal electric gate”, then the energy content of 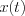$x(t) signal will be changed by 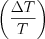$$\left(\frac{\Delta T}{T}\right)$ ratio. In case of ideal sampling is possible to prescribe the equivalence of the energy content between the single element of 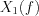$X_1(f) series and 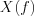$X(f) . It is need to provide the increasing of the transferred energy with the decreasing 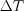$$\Delta T$ . If the amplitude of the switching function will change by 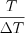$$\frac{T}{\Delta T}$ way, then condition is satisfied.
3.) If in case of ideal sampling 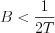$$B<\frac{1}{2T}$ condition is satisfied, then the periodic recurrence spectra won’t overlap each other, consequently the 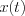$x(t) input signal can be restored without distortion by means of an ideal 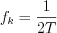$$f_{k}=\frac{1}{2T}$ bandwidth low-pass filter.
4.) If the bandwidth 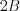$2B and the 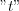sampling time (more generally the sampling aperture) 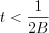$$t<\frac{1}{2B}$ i.e. satisfy the sampling law, then the signal can be restored without distortion independently of the mid-frequency point position. The sampling time (or aperture) is determined by the band-width of the signal not by the high pass frequency limit.

The original document is available at http://549552.cz968.group/tiki-index.php?page=Theory+and+basic+laws+of+sampling