Analysis of linear systems in extended frequency space
The description of linear system will be extended into the complex frequency domain 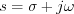 in the following chapters, in order to investigate what kind of association may be created between the various system responses.
in the following chapters, in order to investigate what kind of association may be created between the various system responses.
Definition: Let 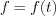 real variable and real as well as complex value general step function:
real variable and real as well as complex value general step function:
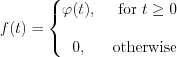 , as well as
, as well as 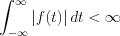
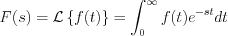 operation is the Laplace transformation of
operation is the Laplace transformation of  . Sufficient condition of Laplace transformation is the
. Sufficient condition of Laplace transformation is the  function should be absolutely integrable (the condition is not necessary, but sufficient).
function should be absolutely integrable (the condition is not necessary, but sufficient).
Laplace transformation is linear, i.e.:
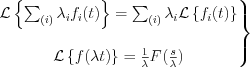 , where
, where 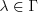
Let’s see, the relation between the Laplace and Fourier transformation. It is known from the above mentioned, the sufficient condition of both Laplace and Fourier transformation is 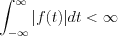 , i.e.
, i.e. 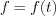 should be absolutely integrable.
should be absolutely integrable.
Fourier transformation: 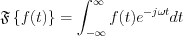
Laplace transformation: 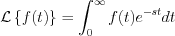
Apply the following substitution in the Laplace transformation expression: 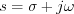 .
.
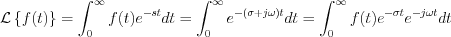
It is known from the definition of Laplace transformation, that 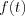 should be general step function. If
should be general step function. If 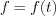 is general step function, then
is general step function, then 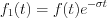 is general step function too.
is general step function too.
Consequently
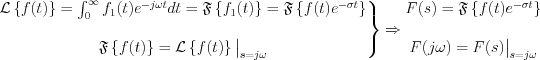
The conclusions are the followings:
Under the conditions, that 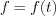 is general step function and absolutely integrable, the Laplace transformation of
is general step function and absolutely integrable, the Laplace transformation of 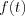 among
among 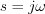 complex axis (i.e. among the imaginary axis) gives the Fourier transformation. Consequently, it is possible to see, the domain of Fourier transformation is the
complex axis (i.e. among the imaginary axis) gives the Fourier transformation. Consequently, it is possible to see, the domain of Fourier transformation is the 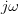 imaginary axis, while the domain of Laplace transformation is the complete complex plane. Another approach is existing also, that the Laplace transformation of
imaginary axis, while the domain of Laplace transformation is the complete complex plane. Another approach is existing also, that the Laplace transformation of 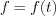 is possible to derive from the Fourier transformation of
is possible to derive from the Fourier transformation of 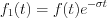 function. Consequently
function. Consequently 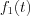 can be expressed by the inverse Fourier transformation as follow:
can be expressed by the inverse Fourier transformation as follow:
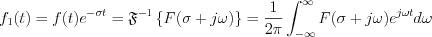
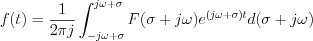
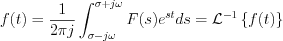 where the expression of inverse Laplace transformation is obtained,
where the expression of inverse Laplace transformation is obtained,
and called Rieman-Melling integral.