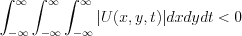Problems (Linear Systems)
1.)
Let 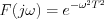 be a Fourier transformation of
be a Fourier transformation of 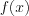 . Determine the inverse Fourier transformation i.e.
. Determine the inverse Fourier transformation i.e. 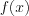 function under the following condition:
function under the following condition:
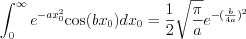
2.)
Determine the Laplace transformation of the following functions:
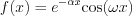 , and
, and 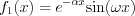
3.)
Determine the inverse Laplace transformation of the following function:
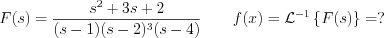
4.)
Find the solution of the following differential equation!
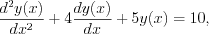
where 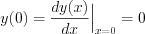 is the initial condition.
is the initial condition.
5.)
Find the solution of the following linear second ordered differential equation!
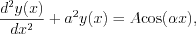 , with the initial conditions
, with the initial conditions 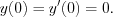
6.)
Find the solution of the following linear third ordered differential equation!
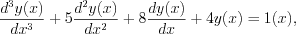 , with the initial conditions
, with the initial conditions 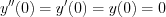
7.)
Let 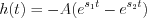 be the step response function of a linear shift invariant system. Determine the system response function if the input function is
be the step response function of a linear shift invariant system. Determine the system response function if the input function is 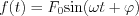 !
!
8.)
Two diagrams of a characteristic transfer function (amplitude and phase) are presented below. Shape-preserving transfer is executing within the 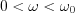 frequency band. Please, determine the weighting function of the linear invariant system.
frequency band. Please, determine the weighting function of the linear invariant system.
9.)
Step response function of a system is : ![$ h(t)= \left [ 2-e^{-5t}+2e^{-10t} \right ] 1(t)](lib/equation/pictures/9a361a09eae8130aa9c587edb9f88c51.png) . Please determine the weighting function of the system!
. Please determine the weighting function of the system!
10.)
Transfer characteristic of a system is as follow:
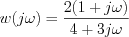
Please determine the step response function of the system by the transfer characteristic!
11.)
Solve the following partial differential equation 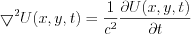 with the following initial conditions
with the following initial conditions
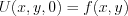
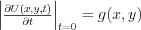
And