Represenation of a Line and other linear geometrical elements
Represenation of a Line and other linear geometrical elements
Line on a plane
On a plane line is a set of x=(x,y) points, where the following expression holds:
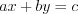 where
where 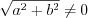 .
.
Equivalently:
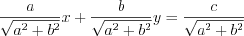
Now the coefficients of x and of y squared add up to 1, we can define the
 unit vector:
unit vector:
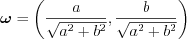
and a t scalar:
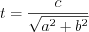
With these notations the expression of a line is:
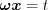 (1)
(1)
Thus, we are looking for the set of o points, where the projection of the location vector to a given  vector is constant.These points are located on a line perpendicular to vector
vector is constant.These points are located on a line perpendicular to vector  , and the distance of this line from the origin is t.
, and the distance of this line from the origin is t.
In order to parametrize the points of this line we look for the 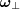 unit vector perpendicular to vector
unit vector perpendicular to vector  . For unique solution let us choose the sign of the determinant of these vectors, now we chose positive:
. For unique solution let us choose the sign of the determinant of these vectors, now we chose positive:
 (2)
(2)
Let us have the variable of integration the point s, with that we obtain the l points of an L line as follows:
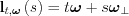
This description still does not constitute a unique description, as when
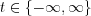 , then
, then 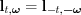 . We should limit either t to positive numbers, or limit
. We should limit either t to positive numbers, or limit  to one of the half-spaces. E.g., when
to one of the half-spaces. E.g., when 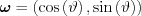 , then either
, then either
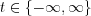 and
and 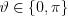
or
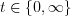 and
and 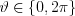
In the literature both conventions are present.
Linear elements in higher dimensions
The expression for the 2D line on 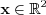 determines sets of points such, that for a
determines sets of points such, that for a 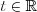 scalar and for a unit vector
scalar and for a unit vector 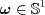 of a sphere of one degree of freedom (
of a sphere of one degree of freedom ( 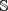 ), the equation holds:
), the equation holds: 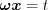 and with that
and with that 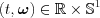 equations determine a line with a direction. When we look at the parametrization of it in Eq. (2), s and t are interchangeable, since
equations determine a line with a direction. When we look at the parametrization of it in Eq. (2), s and t are interchangeable, since  és
és 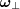 determine each other apart from a sign. We could also say, that the parameter of our line is s and
determine each other apart from a sign. We could also say, that the parameter of our line is s and 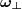 , the variable of integration is t, in the direction of
, the variable of integration is t, in the direction of  .
.
In an n dimension space, Eq. (1) given that 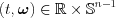 is an expression of a hyperplane perpendicular to the direction vector
is an expression of a hyperplane perpendicular to the direction vector  . Now to specify a single point on this plane, we need a set of direction vectors of a complete base of unit vectors
. Now to specify a single point on this plane, we need a set of direction vectors of a complete base of unit vectors 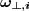 , that we now with an off-hand notation order into matrix
, that we now with an off-hand notation order into matrix 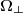 , so now multiplied by a vector of
, so now multiplied by a vector of 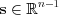 we arrive into a point of the plane as follows:
we arrive into a point of the plane as follows:
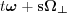
If we choose, like we did before, for the parameters of the linear set 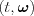 , then our expression describes points of the H hyperplane:
, then our expression describes points of the H hyperplane:
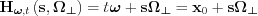
On the contrary, if we chose as the parameters the elements of the product 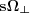 , we obtain a line, with points along unit vector
, we obtain a line, with points along unit vector  with variable of integration t:
with variable of integration t:
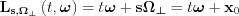
Note, that the points of the H hyperplane is determined by n independent information contained in 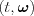 together, while the L line is determined by the product
together, while the L line is determined by the product 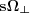
with 2(n-1) independent elements, since additionally to the unit vector we need the values of vector s as well. To reach a point in space we still need to define the vector base of
we need the values of vector s as well. To reach a point in space we still need to define the vector base of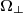 , bearing no information on the object, it only constitutes the coordinate system choice.
, bearing no information on the object, it only constitutes the coordinate system choice.