The 2D Radon transform

Definition

The Radon transform using the notations in the section on the description of linear structures in 2D with $$ \mathbf{x}\in \mathbb{R}^{2}, $ t\in \mathbb{R} , \boldsymbol{\omega}\in \mathbb{S}^{1}$ ) for an f real function:

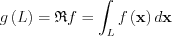
$$ g\left ( L \right )=\mathfrak{R}f =\int_{L}f\left (\textbf{x} \right )d\textbf{x}$

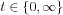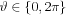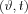Let us follow the convention $$ t\in \left \{ 0,\infty \right \}$ and $$ \vartheta\in \left \{ 0,2\pi \right \}$ , now the function f Radon transformed with variables $$\left ( \vartheta,t \right )}$ :

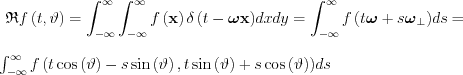
$$ \mathfrak{R}f\left ( t,\vartheta \right )=\int_{-\infty }^{\infty }\int_{-\infty }^{\infty } { f\left ( \mathbf{x} \right )\delta \left ( t-\boldsymbol{\omega} \mathbf{x} \right )}dxdy= \int_{-\infty }^{\infty } { f\left ( t\boldsymbol{\omega}+s\boldsymbol{\omega}_{\perp} \right )}ds = \int_{-\infty }^{\infty } { f\left ( t \cos \left (\vartheta \right ) - s \sin \left (\vartheta \right ) ,t \sin \left (\vartheta \right ) + s \cos \left (\vartheta \right ) \right )}ds$

For the existence of the Radon transform we have to require that the improper integral above exists (more precisely that is integrable in a Lebesgue sense). Johann Radon showed that if f is continuous and has a compact support the Radon transform is unique.

Example

Let us take a "disk" of radius r, where the function values is 1 inside radius r otherwise 0:
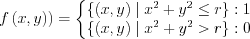
$$ f\left ( x,y \right ))=\left\{ \begin{matrix} \left \{ \left (x,y \right ) \mid x^{2}+y^{2} \leq r\right \} : 1 \\ \left \{ \left (x,y \right ) \mid x^{2}+y^{2} > r\right \} : 0 \end{matrix}\right.$

As the function value is 1 or 0, the Radon transform will be given by the limits of the support: for an arbitrary angle at a given t the nonzero values are on the domain of 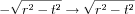$$ -\sqrt{r^{2}-t^{2}} \to \sqrt{r^{2}-t^{2}}$ . Thus:

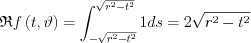
$$ \mathfrak{R}f\left ( t,\vartheta \right )=\int_{-\sqrt{r^{2}-t^{2}} }^{\sqrt{r^{2}-t^{2}} } { 1 } ds = 2\sqrt{r^{2}-t^{2}}$
if t<r and 0 otherwise. The result is independent of angle, has compact support, but despite the original constant function it is not constant.

A 2D Radon transform can be graphed in a 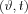$$\left ( \vartheta,t \right )}$ coordinate system, that is called a sinogram, and it is the topic of the next section.

Export

Medical Imaging

Site Language: English

The 2D Radon transform