Timing techniques

 
If two gamma photons are detected ‘simultaneously’, i.e. within a very short time interval, then they were most probably emitted in the same decay. In order to detect the photon pairs simultaneously, we obviously have to know the time of the events (the arrival of the photons) very accurately. Considering that the temporal resolution of a PET system today is 0.5-5 ns, during this time light would cover a distance of 15 cm – 1.5 m. That is how accurately time needs to be measured.

Requirements for coincidence circuits
The incoming events have to be separated from the ever-present noise. That is what the so-called discriminators are for. The basic principle is the following: if a (e.g. PMT) signal meets a criterion (e.g. it has sufficiently high amplitude and/or is sufficiently steep, etc.), then the discriminator generates a trigger signal, thus setting off the rest of the process chain, e.g. storing the sampled values, integrating, calculating the time of arrival, etc. The discriminator is expected to catch the lowest signal possible that is higher than the noise, and the formation of the trigger should be identifiable with the arrival of the event.

Usually there is some sort of stable periodic timing pulse (e.g. 50 MHz) in the detector electronics, which synchronizes the different processing components and data traffic. This in itself is not sufficiently accurate for the timing of events (e.g. a timing pulse of 50 MHz corresponds to 20 ns) but it makes it enough to know the time of the events compared to the synchronizing timing pulse. Basically, our task is to create a ‘stopwatch’ that can accurately measure the time of arrival of a trigger signal compared to the timing pulse. For this the TAC (Time to Amplitude Converter) or its digital counterpart, the TDC (Time to Digital Converter) is used.

 
LE, CFD, TAC
One of the basic types of discriminators used in timing is the LE (Leading Edge) discriminator. It is relatively simple and widespread. In essence it continuously monitors whether the values sampled from the signal reach the predetermined threshold (trigger level) and if they do, it examines if the slope of the leading edge of the signal is sufficiently steep, i.e. if it is plausible that it originated from a scintillation. With adequately steep signals this allows for a relatively good timing, but a basic defect of this is that signals with a higher amplitude are steeper so they reach the trigger level sooner. In other words, the timing of an event depends on the amplitude of the signal. Despite this, timing around 1 ns can usually be achieved; in small animal devices practically exclusively this type of discriminator is used.

Figure 1.

 
In order to reduce the dependence of timing on the amplitude of the signal (energy), Constant Fraction Discriminators (CFDs) are used in case the accuracy of the LE is not sufficient (e.g. positron lifetime measurements, or ToF PET). The basic principle of this is the following: let us generate a reverse replica of the signal with a decreased (f-fold) amplitude, delay the original signal (d) and then let us add up these two. The zero crossing time of the signal generated this way is independent of the amplitude of the signal to a good approximation, if the shape of the low and the high amplitude signals is similar. This can be realized in an analogue electronic way, the trigger is provided by the zero crossing time. Optimizing the rate of decrease (f) and the delay (s) is fairly complicated – it depends on the shape of the signal, the signal-to-noise ratio, etc. – and an incorrectly adjusted CFD is worse than a simple LE discriminator. (There are no theoretical obstacles to realizing all this digitally instead of electronically, however, sampling frequencies in the order of GHz would be needed, which would require very expensive AD converters. Therefore, in practice this is not used in PET scanners.)

Figure 2.

 
If the trigger is generated with the help of a discriminator, the TAC, functioning as a stopwatch, is also needed. The basic principle of this is the following: if a capacitor is charged slowly by a high precision current source (which provides constant current relatively independently of the load), the voltage across the capacitor will be proportional to the elapsed time. Therefore, measuring time will practically mean measuring voltage. When the trigger arrives, the charging of the capacitor of the TAC is started, then it is stopped on the arrival of the next synchronous timing pulse and the amount of charge accumulated on the capacitor is measured. This way (if the line characterizing the voltage increase of the capacitor has previously been calibrated) the time of arrival of the trigger as compared to the next synchronous timing pulse can be determined very precisely. Its digital equivalent, the TDC differs from the TAC in that it contains a fast AD converter as well. It immediately returns a digital timestamp instead of an analogue one.

The theoretical limit of timing
It can be proven that during a scintillation event the atoms are excited practically simultaneously and they relax independently from each other. Every discriminator needs a minimum signal level so that the signal can be distinguished from the noise. Let us presume that the signal-to-noise ratio is such that if the first k photons of a scintillation have arrived, we can already see them, the PMT amplifies the signal higher than the noise. Therefore, k is an arbitrary, fixed number which tells the minimum number of photons that need to arrive so that the generated electrical signal grows above the noise level. (This is the optimal, lowest trigger level possible expressed in the number of photons). In this case, as far as timing is concerned, the following question arises: what is the temporal standard deviation of the time of arrival of the k-th scintillation photon if there are N identical, simultaneously excited atoms that are independent from each other and relax with a probability of p per unit of time?
It can be derived that the standard deviation of the expected time of the relaxation of the first k photons out of N photons is

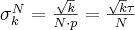
If there are two detectors opposite to each other, the standard deviation of the measurable timing is 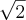times this. Again, it is a matter of the joint standard deviation of two independent random variables. If the time spectrum is Gaussian-like, the full width at half maximum is 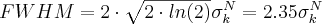, thus the temporal resolution is

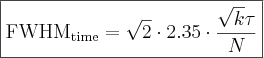
According to this, when timing is based on scintillation light, the full width at half maximum of the time spectrum is inversely proportional to the effective light yield. It is important to note that only those scintillation photons play a role in the statistics that are detected. So N, that has so far been identified with the light yield of the crystal is actually the ‘effective light yield’, which is the product of the light yield of the crystal, the efficiency of the optical arrangement and the detecting efficiency of the detector. The temporal resolution is proportional to the fall time of the crystal and the square root of k, if we consider the arrival of the k-th photon of the scintillation photons as the arrival of the signal. In order to achieve high temporal resolution, a crystal with a high light yield and a fast fall time, a good signal-to-noise ratio and as low a trigger level as possible is needed.