Szonoelasztográfia

Elasztográfiának nevezünk minden olyan képalkotási eljárást, ami az anyag elasztikus tulajdonságait térképezi fel. Azok a módszerek, melyek a képet ultrahang segítségével hozzák létre, a szonoelasztográfiai eljárások.

Anyagok elasztikus tulajdonságai

Különféle anyagok rugalmas tulajdonságait általános alakban a négy-indexes Hooke-tenzor adja meg. Ez a tenzor lineáris összefüggést valósít meg a mechanikai feszültségtenzor és a deformációtenzor elemei között: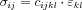
A mechanikai feszültségtenzor diagonális elemei az úgynevezett normális feszültségek (pl. x irányú erő hatására kialakuló x irányú feszültség), míg a főátlón kívüli elemek az anyagban fellépő különféle irányú nyírófeszültségeket jelentik (vagyis például x irányú erő hatására az xy vagy xz síkban fellépő feszültség).
A deformációtenzor diagonális elemeit megkapjuk a főtengelyek mentén mérhető relatív (fajlagos) megnyúlásból, míg a maradék hat elemet az úgynevezett nyírási fajlagos megnyúlásból kapjuk. Képlettel felírva, ha 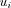vektormező jellemzi az egyes pontok elmozdulását, akkor a deformációtenzor: .
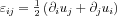Homogén izotróp anyagot feltételezve a Hooke-törvény egyszerűbb alakba írható, számos speciális esetben skaláris összefüggéssé egyszerűsödik. A továbbiakban három, az ultrahang és elasztográfia szempontjából jelentős esetről lesz szó.
Az egyik legismertebb elasztikus mutató a Young-modulus. Ha egy hosszú, vékony rudat húzunk F erővel, akkor a hosszúságának relatív megváltozásához képest a felület megváltozása elhanyagolható. Ebben az esetben a mechanikai feszültség megkapható a húzóerő és a keresztmetszet hányadosaként, míg a deformációt a relatív hosszváltozásból kaphatjuk meg. A két mennyiség hányadosa pedig egy anyagra jellemző állandó, a Young-modulus: E (Pa). Az alábbi ábra szemlélteti a Young-modulus mérési módját:

Egy test minden irányból ható összenyomás hatására térfogatváltozást szenved el. A testre ható nyomás és a relatív térfogatváltozás hányadosa az úgynevezett kompressziómodulus: K (Pa). A következő ábra a kompressziómodulus mérési módját szemlélteti:

A harmadik fontos speciális elasztográfiai mutató a nyírási modulus, G (Pa), amit a nyírófeszültség és a nyírási szög hányadosaként kaphatunk meg. Az alábbi ábrán látható a nyírási modulus egy mérési módja kis nyírási szögek esetén, ekkor ugyanis a szög tangense közel azonos a szög értékével.

A fenti elasztikus modulusok közti összefüggés könnyen felírható az úgynevezett Poisson-tényező segítségével. Ez az érték azt jellemzi, hogy egytengelyű húzófelszültség hatására az adott irányú relatív megnyúláshoz (deformációhoz) képest mekkora a keresztirányú deformáció. Ezt szemlélteti a következő ábra:

A Poisson-tényező és a Young-modulus segítségével felírva a fenti elasztikus modulusokat:

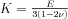
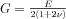
Az elasztográfia elve és típusai

Általánosan ismert tény, hogy a beteg szövetek elasztikus tulajdonságai jelentős eltérést mutatnak az egészséges szövetekhez képest, ezért a tapintás már évszázadok óta használt módja a diagnózisok felállításának. Egyes rákos daganatok, például a mellrák, és a hererák esetében a tumorok nagy keménysége és felszínhez való közelsége miatt a tapintás valóban hatékony módja a betegség felfedezésének, azonban sok esetben, főként mélyebben fekvő elváltozások esetén ez a módszer nem alkalmazható.
Az ultrahang alkalmas a test elasztikus tulajdonságainak feltérképezésére. A hanghullám terjedési sebességének köze van egy elasztikus modulushoz: 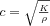, azonban a K kompressziómodulus értéke a különféle szövetekben csupán igen kis eltérést mutat, maximum 1-2%-ot változik. A Young-modulus és a nyírási modulus azonban gyakran több nagyságrendben változik, ahogy ez a táblázatban látható. Ennek oka az, hogy a legtöbb emberi szövet a benne található szabad (extracelluláris) folyadék kinyomása után (ezt nevezzük prekompressziónak) nagyjából összenyomhatatlannak tekinthető.

Szövet/folyadék	K (GPa)	E (kPa)
Máj	2,49	3-10
Cirrózisos máj	2,49	10-50
Vese	2,43	6-10
Átlagos lágyszövet	2,37	0,5-20
Csont	10,89	11000-20000

Az összenyomhatatlanság azt jelenti, hogy az anyag Poisson-tényezője 0,5. A legtöbb lágyszövetre ez az érték 0,49 és 0,499 közé esik, így ez a követelmény többnyire teljesül. Látható, hogy ebben az esetben a kompessziómodulus valóban végtelenhez tart, míg a nyírási modulus és a Young-modulus összefüggése E=3G-re egyszerűsödik.
A fenti okok miatt nem elégséges egyszerűen a szövetekben terjedő hang sebességét megmérni. Nagy általánosságban kétféle eljárást alkalmazunk a Young-modulus illetve a nyírási modulus megmérésére. Egyrészt az ultrahang felvételek alkalmasak arra, hogy direkt módon megmérjük a Young-modulust, ugyanis összenyomott szövetekről készült ultrahangfelvételek alapján a mechanikai deformáció megbecsülhető. A másik eljárás a nyírási modulus mérésére alkalmazható: a szövetekben erősen fókuszált ultrahangimpulzust hozunk létre, ami lökéshullámot indít el. Ez a hullám nyíró jellegű, így sebessége a nyírási modulustól függ: 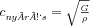. Nyíró hullámot elindíthatunk külső rezgéskeltő eszköz alkalmazásával is. Gyors ultrahang képalkotási eljárások segítségével a nyíráshullám mozgása nyomon követhető, sebessége mérhető, így megkaphatjuk az adott szövetre vonatkozó G modulus értékét.

Az elasztográfiai eljárásoknak számos csoportosítása lehetséges. A fent említett két alapvető csoport legelterjedtebb elnevezése a deformációs elasztográfia (strain elastography), illetve a nyírási elasztográfia (shearwave elastography), mivel az első eljárás a mechanikai deformáció mérésén alapul, míg a második a nyíráshullámok sebességének mérésén. A két csoporton belül számos módszer és kutatási terület alakult ki.

Deformációs elasztográfia
Nyírási elasztográfia

---